曲线积分的计算方法
曲线积分怎样计算

在数学中,曲线积分是一种重要的工具,它用于计算沿着曲线的某些物理量(如质量、力或能量)的累积效果。曲线积分主要分为两类:对弧长的曲线积分(第一型曲线积分)和对坐标的曲线积分(第二型曲线积分)。这两类曲线积分在理论和应用上都有着广泛的应用。以下将详细探讨这两类曲线积分的计算方法及其相关概念。

一、对弧长的曲线积分(第一型曲线积分)
对弧长的曲线积分是计算曲线上某物理量(如密度、温度等)沿曲线分布的累积值。这类积分的计算公式为:

∫_L f(x,y) ds

其中,L 是给定的曲线,f(x,y) 是定义在曲线上的连续函数,ds 是曲线 L 上的弧长元素。
1. 参数化表示
为了计算这个积分,通常需要将曲线 L 参数化,即表示为参数 t 的函数形式:
x = x(t), y = y(t)
其中,t 在某个区间 [a, b] 上变化。这样,弧长元素 ds 可以表示为:
ds = √((dx/dt)^2 + (dy/dt)^2) dt
2. 积分计算
将弧长元素 ds 代入原积分,得到:
∫_L f(x,y) ds = ∫_a^b f(x(t), y(t)) √((dx/dt)^2 + (dy/dt)^2) dt
这是一个关于 t 的一元定积分,可以通过常规的积分方法求解。
3. 示例
假设曲线 L 是单位圆 x^2 + y^2 = 1 的上半部分,f(x,y) = x^2 + y^2。我们可以将曲线 L 参数化为:
x = cos(t), y = sin(t), t ∈ [0, π]
然后计算积分:
∫_L f(x,y) ds = ∫_0^π (cos^2(t) + sin^2(t)) √((-sin(t))^2 + (cos(t))^2) dt = ∫_0^π 1 * dt = π
二、对坐标的曲线积分(第二型曲线积分)
对坐标的曲线积分用于计算向量场沿曲线的线积分,这类积分在物理学中有着重要的应用,如计算力沿曲线的功。计算公式为:
∫_L P(x,y) dx + Q(x,y) dy
其中,L 是给定的曲线,P(x,y) 和 Q(x,y) 是定义在曲线上的连续函数,dx 和 dy 分别是曲线 L 上沿 x 轴和 y 轴方向的微小增量。
1. 参数化表示
同样地,我们需要将曲线 L 参数化,表示为参数 t 的函数形式:
x = x(t), y = y(t)
其中,t 在某个区间 [a, b] 上变化。然后,dx 和 dy 可以表示为:
dx = (dx/dt) dt, dy = (dy/dt) dt
2. 积分计算
将对坐标的曲线积分代入参数化形式,得到:
∫_L P(x,y) dx + Q(x,y) dy = ∫_a^b [P(x(t), y(t)) (dx/dt) + Q(x(t), y(t)) (dy/dt)] dt
这是一个关于 t 的一元定积分,同样可以通过常规的积分方法求解。
3. 格林公式与路径无关性
对于封闭曲线 L(即起点和终点重合的曲线),第二型曲线积分与路径无关,只与曲线所围成的区域 D 有关。这可以通过格林公式来证明:
∮_L P dx + Q dy = ∬_D (∂Q/∂x - ∂P/∂y) dxdy
其中,D 是由曲线 L 所围成的区域。当 P 和 Q 满足一定条件时(即它们在 D 内连续且有一阶连续偏导数),上述公式成立。这意味着,如果两个点 A 和 B 在同一连通区域内,那么从 A 到 B 的第二型曲线积分只与 A、B 两点的位置有关,而与具体路径无关。
4. 示例
假设曲线 L 是直线段,从点 (0,0) 到点 (
- 上一篇: 如何在线轻松申请营业执照
- 下一篇: 揭秘:根号三究竟代表什么?
-
 掌握第一类曲线积分的高效计算方法资讯攻略10-31
掌握第一类曲线积分的高效计算方法资讯攻略10-31 -
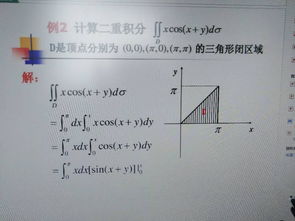 二重积分计算方法揭秘,附上一个简单易懂例题解析资讯攻略12-06
二重积分计算方法揭秘,附上一个简单易懂例题解析资讯攻略12-06 -
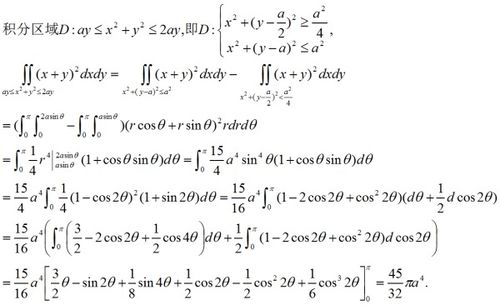 掌握二重积分dxdy的计算方法,轻松解题无烦恼资讯攻略10-24
掌握二重积分dxdy的计算方法,轻松解题无烦恼资讯攻略10-24 -
 双曲线的顶点坐标公式及求解方法资讯攻略10-28
双曲线的顶点坐标公式及求解方法资讯攻略10-28 -
 拉格朗日定理的具体公式是什么资讯攻略11-07
拉格朗日定理的具体公式是什么资讯攻略11-07 -
 如何绘制最速曲线资讯攻略01-23
如何绘制最速曲线资讯攻略01-23