求解方程的六个关键公式

解方程的六个基本公式是学习代数时不可或缺的工具，这些公式不仅能够帮助我们理解和解决各种数学问题，还能应用于实际生活中的计算。以下是关于解方程六个公式的详细介绍，适合对数学尤其是代数感兴趣的读者。

首先，让我们了解一下什么是方程。方程是一个包含未知数和等号的数学表达式，例如“x + 5 = 10”。解方程的过程就是找出使这个表达式成立的未知数的值。在这个过程中，我们会用到六个基本的公式，这些公式帮助我们处理不同类型的方程。

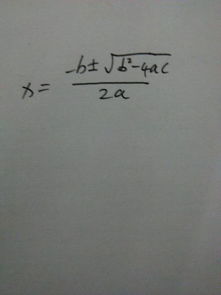
第一个公式：一个加数=和-另一个加数

这个公式适用于加法方程。当我们面对形如“a + b = c”的方程时，可以通过减去已知的一个加数b来找到另一个加数a的值。同样，我们也可以用这个公式来解出方程中的未知数。例如，如果方程是“x + 3 = 7”，那么我们就可以通过“7 - 3”来找到x的值，即x = 4。

第二个公式：被减数=差+减数

这个公式用于处理减法方程。当我们知道方程中的差和减数，而需要找出被减数时，可以使用这个公式。例如，如果方程是“x - 5 = 3”，我们就可以通过“3 + 5”来找到x的值，即x = 8。这个公式同样适用于解决包含未知数的减法问题。

第三个公式：减数=被减数-差

这个公式用于求解减法方程中的减数。当我们知道被减数和差，但不知道减数时，这个公式非常有用。例如，如果方程是“10 - x = 4”，我们就可以通过“10 - 4”来找到x的值，即x = 6。

第四个公式：一个因数=积÷另一个因数

在处理乘法方程时，这个公式非常关键。如果我们知道两个数的乘积，以及其中一个因数，就可以用这个公式来找出另一个因数。例如，如果方程是“4x = 20”，我们就可以通过“20 ÷ 4”来找到x的值，即x = 5。这个公式对于解决涉及未知数的乘法问题同样有效。

第五个公式：被除数=商×除数

这个公式用于处理除法方程。当我们知道商和除数，而需要找出被除数时，这个公式非常有用。例如，如果方程是“x ÷ 3 = 7”，我们就可以通过“7 × 3”来找到x的值，即x = 21。这个公式同样适用于解决包含未知数的除法问题。

第六个公式：除数=被除数÷商

这个公式用于求解除法方程中的除数。当我们知道被除数和商，但不知道除数时，这个公式就派上了用场。例如，如果方程是“28 ÷ x = 4”，我们就可以通过“28 ÷ 4”来找到x的值，即x = 7。

除了上述六个基本公式外，还有一些其他的数学原理和技巧可以帮助我们解决更复杂的方程。例如，公式法是一种直接利用已知公式来求解方程的方法。对于一些已经研究出解的一般形式的方程，我们可以直接套用公式来求解。例如，一元二次方程ax² + bx + c = 0的解可以通过公式x = [-b ± √(b² - 4ac)] / (2a)来求解，其中a、b和c是方程的系数。

因式分解法是另一种常用的解方程技巧。这种方法通过将方程变形为一边是零，另一边是二次三项式的形式，然后将二次三项式分解成两个一次因式的积，从而得到两个一元一次方程，解这两个一元一次方程就可以得到原方程的两个根。例如，对于方程x² - 3x + 2 = 0，我们可以将其分解为(x - 1)(x - 2) = 0，然后分别解x - 1 = 0和x - 2 = 0，得到x = 1和x = 2作为原方程的解。

此外，函数图像法也是解决方程的一种有效方法。这种方法利用方程的解为两个以上关联函数图像的交点的几何意义来求解。例如，对于一元二次方程，我们可以将其转化为函数y = ax² + bx + c和y = 0的图像交点问题，通过观察和分析函数图像来找到方程的解。

除了这些具体的解方程技巧外，还有一些数学原理和公式对于理解和解决方程也非常重要。例如，整式运算公式、分式运算公式以及几何公式等，都是我们在学习和应用数学时不可或缺的工具。这些公式不仅能够帮助我们解决数学问题，还能培养我们的逻辑思维和数学素养。

在学习和应用这些公式时，我们需要注意以下几点：

1. 理解公式的含义和适用范围：每个公式都有其特定的含义和