探索毕达哥拉斯树的奥秘:几何画板绘制实战指南
毕达哥拉斯树,又称勾股树,是一种基于勾股定理构建的、可以无限重复的树形几何图形。因其形状在重复绘制后宛如一棵枝繁叶茂的大树而得名。利用几何画板这一强大的几何绘图工具,我们可以轻松绘制出这一充满数学魅力的图形。以下将详细介绍如何在几何画板中绘制毕达哥拉斯树。

首先,启动几何画板。在桌面左下角点击“开始”按钮,选择“所有程序”,找到并启动“GSP4.05”应用程序。几何画板提供了丰富的绘图工具,包括点工具、直尺工具、圆规工具等,可以方便地绘制点、线、圆等基本几何元素。

第一步:绘制初始线段

1. 在几何画板的新建文件中,使用“点工具”在绘图区任意位置点击两次,绘制出两个点A和B。

2. 使用“直尺工具”连接点A和点B,绘制出线段AB。
第二步:设置旋转中心
1. 双击点A,将其标记为旋转中心。
2. 选中点B,选择菜单栏中的“变换”选项,再选择“旋转”命令。在弹出的对话框中,设置旋转角度为90度,点击“旋转”按钮,得到点B'。
3. 双击点B',将其标记为新的旋转中心。
4. 选中点A,再次选择“变换”中的“旋转”命令,设置旋转角度为-90度,点击“旋转”按钮,得到点A'。
第三步:绘制旋转后的线段
1. 使用“直尺工具”连接点A和点B',绘制出线段AB'。
2. 同样地,连接点B'和点A',绘制出线段B'A'。
第四步:构造中点与圆
1. 选中线段B'A',选择“构造”选项中的“中点”命令,绘制出线段B'A'的中点C。
2. 依次选中点C和点A',选择“构造”中的“以圆心和圆周上点绘圆”命令,绘制出以点C为圆心、点A'在圆周上的圆C。
第五步:构造圆上的弧与点
1. 选中点A'、B'和圆C,选择“构造”中的“圆上的弧”命令,绘制出圆C上的一段弧。
2. 保持弧的选中状态,选择“构造”中的“弧上的点”命令,在弧上任意绘制出点D。
第六步:隐藏部分对象与设置线型
1. 将圆C、点C、半圆弧以及线段A'B'隐藏,使图形更加简洁。
2. 将线段BA'的线型设置为粗线,使其更加突出。
第七步:构造线段与度量距离
1. 构造线段B'D,并选中它,选择“度量”中的“距离”命令,度量出线段B'D的长度。
第八步:填充四边形与设置颜色
1. 选中点A、B、A'、B',选择“构造”中的“四边形内部”命令,填充四边形ABA'B'的内部。
2. 选中四边形ABA'B'的内部以及线段B'D的长度,选择“显示”中的“颜色”选项,再选择“参数”命令。在弹出的对话框中,采用默认设置,点击确定,为四边形填充颜色。
第九步:设置动画
1. 选中点D,选择“编辑”中的“操作类按钮”选项,再选择“动画”命令。在弹出的对话框中,将方向栏设置为“向前”,然后点击确定,为点D设置一个动画按钮。
第十步:设置迭代
1. 选中点A和点B,选择“变换”中的“迭代”命令。
2. 在弹出的迭代对话框中,依次点击点B'、点D,作为第一次迭代的映射点。
3. 选择“结构”中的“添加新的映射”命令,再依次点击点D、点A',作为第二次迭代的映射点。
4. 在“显示”中可以增加或减少迭代的次数,根据需要调整。
5. 点击“迭代”按钮,完成迭代设置。
至此,毕达哥拉斯树的绘制就完成了。点击“运动点”的按钮时,随着点的运动,图案会发生变化,展示出毕达哥拉斯树的动态美。
毕达哥拉斯树不仅是一个美丽的几何图形,更是勾股定理的直观体现。通过几何画板的绘制过程,我们可以更加深入地理解勾股定理的应用,以及如何通过几何变换构造出复杂的图形。
在绘制过程中,需要注意以下几点:
1. 准确选择对象:在每一步操作中,都需要准确选择需要操作的对象,如点、线段、圆等。
2. 正确设置参数:在旋转、迭代等操作中,需要正确设置参数,如旋转角度、迭代次数等。
3. 合理隐藏对象:为了使图形更加简洁明了,需要合理隐藏部分对象,如辅助线、临时点等。
4. 灵活调整样式:可以根据需要调整图形的样式,如线型、颜色等,使图形更加美观。
几何画板作为一款功能强大的几何绘图工具,不仅可以帮助我们绘制出各种复杂的几何图形,还可以通过动画、迭代等功能展示图形的动态变化。通过学习和掌握几何画板的使用技巧,我们可以更加深入地理解几何学的奥秘,享受数学带来的乐趣。
毕达哥拉斯树的绘制过程不仅是一次数学实践,更是一次数学美的探索。在这个过程中,我们不仅可以学习到几何图形的构造方法,还可以感受到数学与艺术的完美结合。希望本文的介绍能够帮助读者更好地理解和掌握几何画板绘制毕达哥拉斯树的操作技巧,享受数学带来的无穷魅力。
- 上一篇: 毕业证明书申办全攻略
- 下一篇: 万和电热水器使用指南:轻松上手教程
-
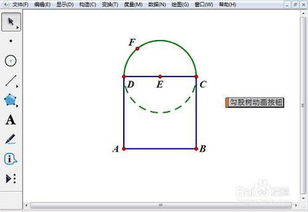 勾股树绘制教程:利用几何画板实现资讯攻略01-12
勾股树绘制教程:利用几何画板实现资讯攻略01-12 -
 揭秘圆周率:探寻隐藏的数学奥秘与规律资讯攻略11-19
揭秘圆周率:探寻隐藏的数学奥秘与规律资讯攻略11-19 -
 绘制家族树的创意指南资讯攻略11-15
绘制家族树的创意指南资讯攻略11-15 -
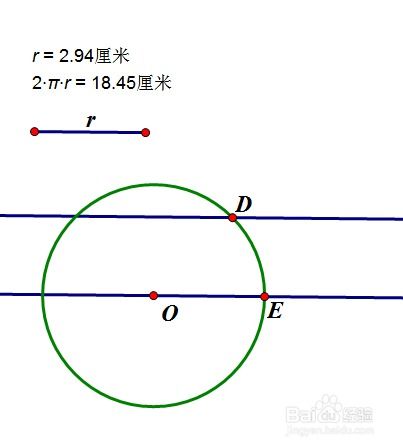 如何用几何画板构造正弦波?资讯攻略10-31
如何用几何画板构造正弦波?资讯攻略10-31 -
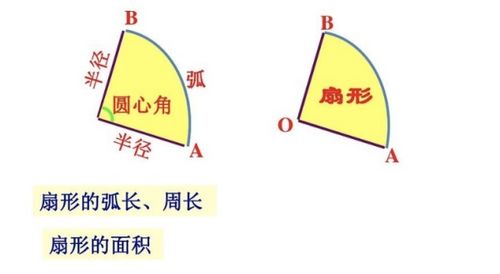 揭秘扇形弧长的计算方法,轻松掌握几何奥秘!资讯攻略11-19
揭秘扇形弧长的计算方法,轻松掌握几何奥秘!资讯攻略11-19 -
 如何绘制春日美景图资讯攻略11-24
如何绘制春日美景图资讯攻略11-24









