三次方方程如何判断是否有解?
在数学的浩瀚宇宙中,立方方程(或称三次方程)如同一颗璀璨的星辰,吸引着无数探索者的目光。当我们面对形如ax³+bx²+cx+d=0(a≠0)的方程时,心中总会涌起一个疑问:这个方程真的有解吗?如何找到这些解?别急,让我们一同踏上寻找答案的奇妙旅程,揭开三次方程是否有解的神秘面纱。

一、三次方程的初步探索

首先,我们要明白,三次方程与一次方程、二次方程相比,其复杂度有了质的飞跃。一次方程ax+b=0的解可以通过简单的除法求得,二次方程ax²+bx+c=0的解则依赖于著名的求根公式(韦达定理)。而三次方程,它的解法并非一眼就能看穿,而是经历了漫长岁月中无数数学家的智慧碰撞,才最终得以揭示。
历史上,首次系统研究三次方程解法的是意大利数学家卡尔达诺(Cardano),在他的著作《大术》中,详细记录了求解三次方程的复杂过程。但在此之前,许多数学家如塔塔利亚(Tartaglia)和费拉里(Ferrari)也对此进行了深入探讨。

二、判别式的引入——判断是否有实根的钥匙
面对三次方程,我们首先需要一个工具来判断它是否有实数解。这个工具就是判别式(Discriminant)。与二次方程中的判别式Δ=b²-4ac类似,三次方程的判别式更为复杂,但它同样能够告诉我们方程的根的性质。
对于一般形式的三次方程ax³+bx²+cx+d=0,我们可以先通过变量替换将其转化为缺项形式(即消去x²项),得到y³+py+q=0。此时,判别式Δ=-(4p³+27q²)便成为了我们判断方程是否有实数解的关键。
当Δ>0时,方程有三个不同的实数解(或者有一个实数解和两个共轭复数解,但这里我们只关注实数解的情况)。
当Δ=0时,方程至少有两个相同的实数解(可能是三个相同的实数解,或者两个相同的实数解和一个不同的实数解)。
当Δ<0时,方程没有实数解,只有三个共轭的复数解。
三、卡尔达诺公式的魅力——求解三次方程的魔法
既然有了判别式来判断方程是否有实数解,那么接下来我们就需要一套方法来具体求解这些解。这时,卡尔达诺公式便粉墨登场了。
对于缺项形式的三次方程y³+py+q=0,卡尔达诺公式给出了一个优雅的解的形式:
y1 = -[(q/2 + √(Δ/4))^(1/3)] + [(q/2 - √(Δ/4))^(1/3)]
y2, y3 是y1的复数共轭,或者当Δ≥0时,可以通过适当的变换得到另外两个实数解。
这个公式看起来有些复杂,但它实际上是将复杂的三次方程求解过程简化为对几个基本运算(加法、减法、乘法、除法、开立方)的组合使用。需要注意的是,这里的开立方运算可能会涉及复数,因此在实际应用中需要谨慎处理。
四、特殊情况的处理——当方程更简单时
虽然卡尔达诺公式可以求解一般的三次方程,但在某些特殊情况下,我们可以找到更简单的解法。例如:
当方程可以因式分解为(x-α)(x-β)(x-γ)=0时,我们可以直接求出α、β、γ作为方程的解。
当方程是形如x³=a的形式时,解就是x=a^(1/3)(这里同样需要注意a可能是负数或复数的情况)。
对于形如x³+px+q=0且p、q为特定关系的方程(如p²=3q等),也可以通过特定的变换和技巧找到解。
五、实际应用中的三次方程
三次方程不仅在数学理论中占有一席之地,在实际应用中也扮演着重要角色。例如:
在物理学中,三次方程可以用来描述某些振动系统的运动规律。
在经济学中,它可以用来分析供需平衡点的稳定性问题。
在化学工程中,三次方程可以用来模拟某些化学反应的动力学过程。
此外,在几何学、计算机科学等领域,三次方程也有着广泛的应用。可以说,三次方程是连接数学理论与现实世界的一座桥梁。
六、结语:探索永无止境
通过对三次方程是否有解以及如何求解的探讨,我们不仅领略了数学世界的奇妙与深邃,也感受到了数学在实际应用中的巨大价值。然而,数学的探索之路是永无止境的。即使我们已经掌握了三次方程的解法,仍然有许多未知的数学领域等待着我们去探索、去发现。
在未来的日子里,或许会有更多更高效的求解三次方程的方法被提出;或许我们会发现
- 上一篇: 哪个国家的国旗上有蓝色加号?
- 下一篇: QQ注册登录后的实名认证全攻略
-
 轻松掌握!一元一次方程解法大全资讯攻略11-04
轻松掌握!一元一次方程解法大全资讯攻略11-04 -
 如何判断一个方程是否有实数根?资讯攻略11-29
如何判断一个方程是否有实数根?资讯攻略11-29 -
 如何轻松掌握二元一次方程的解题步骤?资讯攻略12-05
如何轻松掌握二元一次方程的解题步骤?资讯攻略12-05 -
 二元一次方程的求解方法资讯攻略12-05
二元一次方程的求解方法资讯攻略12-05 -
 掌握解二元一次方程的四大高效方法资讯攻略11-26
掌握解二元一次方程的四大高效方法资讯攻略11-26 -
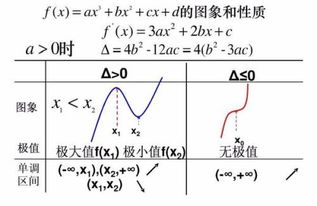 揭秘三次函数的图像奥秘与独特性质资讯攻略11-04
揭秘三次函数的图像奥秘与独特性质资讯攻略11-04











