什么是阶乘以及10的阶乘是多少?
在数学的世界里,阶乘是一个既基础又充满魅力的概念。它不仅仅是一个简单的数学运算,更是连接了数学、物理学、计算机科学等多个领域的桥梁。今天,我们就来深入探讨一下“什么叫阶乘”,并以10的阶乘为例,从多个维度来解析这一数学概念。

阶乘的定义与起源
阶乘,用数学符号表示为“!”,是一个从自然数映射到自然数的函数。对于任意非负整数n,n的阶乘定义为所有小于等于n的正整数的乘积。用数学公式表示就是:n! = n × (n-1) × (n-2) × ... × 2 × 1。特别地,0的阶乘被定义为1,即0! = 1。
阶乘的概念最早可以追溯到17世纪的欧洲,由数学家们在对组合数学和概率论的研究中逐渐明确。尽管在古代的印度和中国,类似的乘积运算也曾在某些数学问题中出现,但现代意义上的阶乘概念及其符号“!”是在近代数学发展中形成的。
阶乘与组合数学
阶乘在组合数学中扮演着至关重要的角色。组合数学是研究离散结构和组合对象的数学分支,而阶乘则是计算排列和组合数量的基础工具。例如,从n个不同元素中取出k个元素的所有排列数可以用n!/(n-k)!来计算,而从n个不同元素中取出k个元素的所有组合数则可以用n!/[k!(n-k)!]来计算。
以10的阶乘为例,10! = 10 × 9 × 8 × ... × 2 × 1 = 3628800。这个数值在组合数学中有着广泛的应用。比如,它表示了从10个不同元素中取出10个元素的所有排列数。换句话说,如果你有10个不同的物品,那么这10个物品的所有可能排列方式就有3628800种。
阶乘与概率论
在概率论中,阶乘也扮演着重要的角色。特别是在计算某些特定事件的概率时,阶乘往往是不可或缺的。例如,在经典的“生日悖论”中,我们可以利用阶乘来计算在一个人数固定的群体中,存在至少两个人生日相同的概率。
此外,阶乘还与泊松分布、二项分布等概率分布密切相关。这些分布是概率论和统计学中的基本概念,广泛应用于质量控制、保险风险评估、网络流量分析等领域。在这些分布的概率质量函数或累积分布函数中,阶乘往往作为关键的计算因子出现。
阶乘与计算机科学
在计算机科学中,阶乘也是一个重要的数学概念。特别是在算法设计和复杂度分析中,阶乘经常被用来评估算法的时间复杂度和空间复杂度。例如,在解决某些递归问题时,算法的时间复杂度可能与输入规模的阶乘成正比。
此外,阶乘也是计算机科学中许多经典问题的基础。比如,在排列生成问题中,我们需要生成一个集合的所有可能排列,而排列的数量正好等于该集合元素个数的阶乘。在解决这类问题时,我们通常需要设计高效的算法来避免重复生成相同的排列,并确保所有可能的排列都能被生成。
阶乘与物理学
虽然阶乘在物理学中的直接应用不如在数学和计算机科学中那么显著,但它仍然在某些物理问题的求解过程中发挥着重要作用。特别是在量子力学和统计物理中,阶乘经常出现在对多粒子系统的描述和计算中。
例如,在玻色-爱因斯坦统计和费米-狄拉克统计中,我们需要计算粒子在不同能级上的分布概率。这些概率通常与粒子的阶乘有关,因为粒子在这些统计中的行为是遵循对称性或反对称性的。此外,在量子场论中,阶乘也出现在对粒子数态的描述和计算中。
阶乘的计算与优化
对于较小的自然数n,我们可以直接通过乘法运算来计算n的阶乘。然而,当n较大时,直接计算阶乘会变得非常耗时和占用大量内存。因此,在实际应用中,我们通常需要采用一些优化算法来计算大数的阶乘。
一种常见的优化方法是使用递归算法。递归算法通过将一个较大的问题分解为若干个较小的问题来求解,从而避免了直接计算大数的阶乘。然而,递归算法也可能导致栈溢出等问题,因此需要谨慎设计。
另一种优化方法是使用迭代算法。迭代算法通过循环结构来逐步累乘得到阶乘的结果,从而避免了递归算法中的栈溢出问题。在实际应用中,我们通常会根据具体的计算需求和资源限制来选择合适的算法。
此外,还有一些更高级的优化方法,如使用大数库、并行计算等。这些方法可以进一步提高计算大数阶乘的效率和准确性。
结语
综上所述,阶乘是一个既基础又充满魅力的数学概念。它不仅在数学领域有着广泛的应用,而且在物理学、计算机科学等多个领域也发挥着重要作用。通过深入了解阶乘的定义、性质和应用,我们可以更好地把握这些领域中的相关问题和挑战。同时,我们也可以通过不断优化阶乘的计算方法,来提高解决这些问题的效率和准确性。在未来的学习和研究中,让我们继续探索阶乘的奥秘,为科学和技术的发展贡献自己的力量。
- 上一篇: 轻松掌握!单书名号键盘输入技巧揭秘
- 下一篇: 揭秘打码:轻松赚钱的神秘数字迷雾
-
-
 如何计算C21资讯攻略12-07
如何计算C21资讯攻略12-07 -
 M10标准螺纹规格是多少资讯攻略11-01
M10标准螺纹规格是多少资讯攻略11-01 -
 10G流量等于多少兆及可用时长解析资讯攻略12-07
10G流量等于多少兆及可用时长解析资讯攻略12-07 -
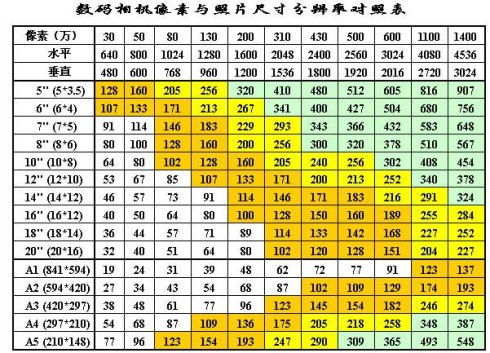 四寸照片的尺寸是多少资讯攻略10-26
四寸照片的尺寸是多少资讯攻略10-26 -
 揭秘:10万万元究竟等同于多少亿?资讯攻略11-03
揭秘:10万万元究竟等同于多少亿?资讯攻略11-03












