扇形的所有重要公式汇总
扇形,作为一种基本的几何图形,其定义、性质和计算公式在几何学中占据重要地位。本文将详细探讨扇形的全部公式,从面积、弧长、周长和角度等多个维度进行阐述,帮助读者深入理解并掌握扇形相关的几何知识。
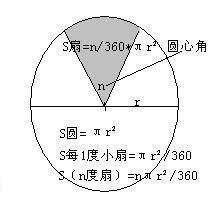
扇形的定义与基本性质
扇形是由一条圆弧和经过这条圆弧两端的两条半径所围成的图形。也就是说,扇形是由圆心角、半径和所对的弧所共同确定的区域。在等圆或等半径的圆中,相等的圆心角所对的弧相等、弦相等、弦心距也相等。这些性质为扇形的研究提供了基础。

扇形的面积公式
扇形面积的计算是几何学中的基本问题之一。扇形的面积可以通过多种方式计算:
1. 面积公式(角度制):
\[
S = \frac{n\pi R^2}{360}
\]
其中,\(S\) 是扇形面积,\(n\) 是圆心角的度数,\(R\) 是扇形半径,\(\pi\) 是圆周率,约为3.14。
2. 面积公式(弧长制):
\[
S = \frac{LR}{2}
\]
其中,\(L\) 是扇形的弧长,\(R\) 是扇形半径。这一公式是通过将扇形面积视为一个小的矩形区域(其中弧长作为矩形的一边,半径作为另一边),然后通过微积分的方法推导出来的。
3. 面积公式(圆面积比例制):
扇形面积也可以通过扇形所在圆的面积除以360再乘以扇形圆心角的角度\(n\)来计算。具体公式为:
\[
S = \frac{\pi R^2}{360} \times n
\]
这一公式实质上是第一种面积公式的另一种表述方式。
扇形的弧长公式
扇形的弧长是指扇形所对应的圆弧的长度。弧长的计算公式同样有多种表述方式:
1. 弧长公式(角度制):
\[
L = \frac{n\pi R}{180}
\]
其中,\(L\) 是弧长,\(n\) 是圆心角的度数,\(R\) 是半径,\(\pi\) 是圆周率。
2. 弧长公式(弧度制):
如果圆心角用弧度来表示,那么弧长的计算公式为:
\[
L = \alpha R
\]
其中,\(\alpha\) 是圆心角的弧度数的绝对值,\(R\) 是半径。
扇形的周长公式
扇形的周长是指扇形的边界线的总长度,包括两条半径和一段圆弧。扇形的周长计算公式为:
1. 周长公式:
\[
C = 2R + L
\]
其中,\(C\) 是扇形的周长,\(R\) 是半径,\(L\) 是扇形的弧长。
如果圆心角的度数\(n\)已知,那么弧长\(L\)可以通过弧长公式计算出来,从而得到扇形的周长公式:
\[
C = 2R + \frac{n\pi R}{180} = 2R + \frac{n}{180} \pi R = R \left( 2 + \frac{n\pi}{180} \right)
\]
扇形角度公式
扇形角度是指扇形所对应的圆心角的度数。扇形角度可以通过扇形的面积和半径来计算:
1. 角度公式:
\[
n = \frac{S}{\pi R^2} \times 360
\]
其中,\(n\) 是圆心角的度数,\(S\) 是扇形面积,\(R\) 是半径,\(\pi\) 是圆周率。
扇形的应用与实例
扇形不仅在数学和几何学中占据重要地位,而且在工程、物理、天文学等领域有广泛应用。以下是一些扇形应用的具体实例:
1. 扇形天线:
扇形天线是一种用于无线通信的天线形式,其形状类似扇形,具有定向性强、增益高等特点。
2. 扇形齿轮:
扇形齿轮是一种常见的齿轮类型,广泛应用于机械传动系统中,用于传递扭矩和改变转速。
3. 扇形叶片:
扇形叶片是风力发电机和风扇等设备中的关键部件,通过旋转产生风能和风力,实现能量转换。
4. 扇形统计图:
扇形统计图是一种常用的统计图表类型,通过扇形面积表示各部分所占的比例,直观地展示数据的分布情况。
总结
扇形作为一种基本的几何图形,其定义、性质和计算公式在几何
- 上一篇: 台湾有多大面积?相当于哪个省份的面积?
- 下一篇: 搜狗输入法:轻松开启斗图新境界!
-
 高中数学:轻松掌握扇形弧长和面积公式资讯攻略11-08
高中数学:轻松掌握扇形弧长和面积公式资讯攻略11-08 -
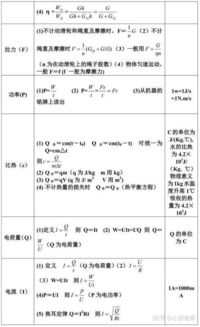 资料分析常用公式有哪些汇总?资讯攻略11-02
资料分析常用公式有哪些汇总?资讯攻略11-02 -
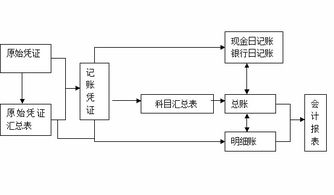 如何轻松上手编制科目汇总表?详细步骤揭秘!资讯攻略10-25
如何轻松上手编制科目汇总表?详细步骤揭秘!资讯攻略10-25 -
 一问一答揭秘:科目汇总表如何正确填写?资讯攻略10-26
一问一答揭秘:科目汇总表如何正确填写?资讯攻略10-26 -
 美国各州中英文名称汇总资讯攻略11-25
美国各州中英文名称汇总资讯攻略11-25 -
 Excel中分类汇总的操作方法资讯攻略12-02
Excel中分类汇总的操作方法资讯攻略12-02











