资料分析常用公式有哪些汇总?
资料分析是数据驱动决策的关键步骤,它涉及从原始数据中提取有用信息,并通过一系列计算和分析方法转化为有价值的洞见。在这个过程中,公式汇总扮演着至关重要的角色,它们为数据分析提供了理论基础和计算工具。本文旨在介绍资料分析中常用的公式汇总,并通过结构化的内容布局和关键词布局,提高文章的阅读体验和搜索引擎友好度。
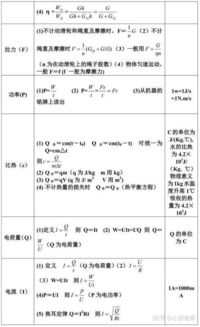
在资料分析中,基础的数学和统计学公式是必不可少的。首先,我们介绍几类基本且常用的计算:

一、平均数

平均数是衡量数据集中心位置的一个简单而有效的指标。常见的平均数包括算术平均数、几何平均数和调和平均数。
1. 算术平均数:
\[
\text{算术平均数} = \frac{\sum_{i=1}^{n} x_i}{n}
\]
其中,\(x_i\)表示每个观测值,\(n\)表示观测值的数量。
2. 几何平均数:
\[
\text{几何平均数} = \sqrt[n]{\prod_{i=1}^{n} x_i}
\]
适用于所有观测值均为正数的情况。
3. 调和平均数:
\[
\text{调和平均数} = \frac{n}{\sum_{i=1}^{n} \frac{1}{x_i}}
\]
常用于计算平均速率等问题。
二、方差与标准差
方差和标准差用于衡量数据集的离散程度。
1. 方差:
\[
\text{方差} = \frac{\sum_{i=1}^{n} (x_i - \mu)^2}{n}
\]
其中,\(\mu\)表示算术平均数。
2. 标准差:
\[
\text{标准差} = \sqrt{\text{方差}}
\]
三、比例与百分比
比例和百分比常用于描述部分与整体的关系。
1. 比例:
\[
\text{比例} = \frac{\text{部分}}{\text{整体}}
\]
2. 百分比:
\[
\text{百分比} = \left(\frac{\text{部分}}{\text{整体}}\right) \times 100\%
\]
四、增长率与下降率
增长率与下降率用于衡量数值随时间变化的幅度。
1. 增长率:
\[
\text{增长率} = \left(\frac{\text{现期值}}{\text{基期值}} - 1\right) \times 100\%
\]
2. 下降率:
\[
\text{下降率} = \left(1 - \frac{\text{现期值}}{\text{基期值}}\right) \times 100\%
\]
五、相关性分析
相关性分析用于评估两个变量之间的线性关系强度和方向。
1. 相关系数:
\[
r = \frac{\sum_{i=1}^{n} (x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum_{i=1}^{n} (x_i - \bar{x})^2 \sum_{i=1}^{n} (y_i - \bar{y})^2}}
\]
其中,\(r\)的取值范围为-1到1,接近1表示正相关,接近-1表示负相关,接近0表示无相关。
六、回归分析
回归分析用于描述和预测变量之间的依赖关系。
1. 简单线性回归方程:
\[
\hat{y} = \beta_0 + \beta_1 x
\]
其中,\(\hat{y}\)表示因变量的预测值,\(\beta_0\)表示截距,\(\beta_1\)表示斜率。
七、时间序列分析
时间序列分析用于研究随时间变化的数据序列。
1. 移动平均法:
\[
\text{移动平均值} = \frac{\sum_{i=k-n+1}^{k} x_i}{n}
\]
其中,\(x_i\)表示时间序列中的数据点,\(n\)表示移动平均的窗口大小。
八、指数分析
指数分析用于反映现象在不同时期的变化方向和程度。
1. 指数公式:
\[
\text{指数} = \frac{\text{现期值}}{\text{基期值}} \times 10
- 上一篇: 轻松上手:自制美味羊杂汤的详细步骤
- 下一篇: 中国传统节日及风俗都有哪些?
-
 资料分析中的比重计算公式是什么?资讯攻略11-08
资料分析中的比重计算公式是什么?资讯攻略11-08 -
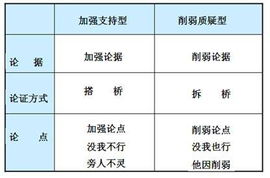 论证思路常用答题模板汇总资讯攻略11-16
论证思路常用答题模板汇总资讯攻略11-16 -
 三阶魔方还原有哪些常用公式?资讯攻略11-08
三阶魔方还原有哪些常用公式?资讯攻略11-08 -
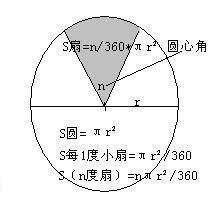 扇形的所有重要公式汇总资讯攻略10-28
扇形的所有重要公式汇总资讯攻略10-28 -
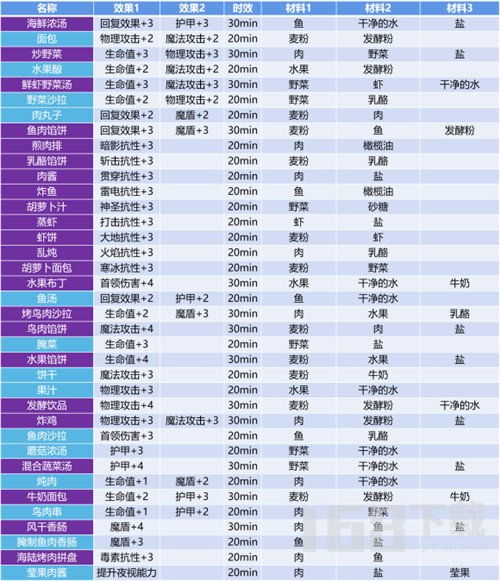 地下城堡3中有哪些食谱配方汇总?资讯攻略12-03
地下城堡3中有哪些食谱配方汇总?资讯攻略12-03 -
 如何计算平均数?资讯攻略10-28
如何计算平均数?资讯攻略10-28












