等腰三角形判定技巧大揭秘
等腰三角形的判定方法是几何学中的一个基础而重要的内容。了解并掌握这些方法,不仅能加深我们对三角形性质的理解,还能在实际解题中起到事半功倍的效果。以下是等腰三角形判定的几种常用方法:
方法一:根据定义判定
等腰三角形是指有两边长度相等的三角形。换句话说,如果三角形ABC满足AB=AC(或BC=BA,或CA=CB),则三角形ABC是等腰三角形。

示例
设三角形ABC,已知AB=5厘米,AC=5厘米,BC=6厘米。根据等腰三角形的定义,AB=AC,所以三角形ABC是等腰三角形。

方法二:根据等腰三角形的性质判定
等腰三角形有一些独特的性质,这些性质也可以反过来用于判定一个三角形是否是等腰三角形。
性质1:等腰三角形的两个底角相等
如果三角形ABC的两个角∠B和∠C相等(即∠B=∠C),则三角形ABC的两边AB和AC也相等,因此三角形ABC是等腰三角形。
示例
设三角形ABC,已知∠B=60°,∠C=60°,∠A=60°。因为∠B=∠C,所以三角形ABC的两边AB和AC相等,三角形ABC是等腰三角形。
性质2:等腰三角形的三线合一
等腰三角形底边上的中线、底边上的高以及顶角的角平分线互相重合。如果三角形ABC中有一条线段既是底边BC的中线,又是BC边上的高,或者是∠A的角平分线,则三角形ABC是等腰三角形。
示例
设三角形ABC,AD是BC边上的中线,同时也是BC边上的高和∠A的角平分线。根据等腰三角形的性质,三角形ABC是等腰三角形。
方法三:根据边角关系判定
在一些特定情况下,我们可以利用三角形的边角关系来判定一个三角形是否是等腰三角形。
判定定理1:边角边(SAS)
如果两个三角形有两边及它们之间的夹角相等,则这两个三角形全等。利用这个定理,如果三角形ABC的两边AB和AC与它们之间的夹角∠A满足AB=AC(或BC=BA,或CA=CB)且∠A=∠B(或∠A=∠C,或∠B=∠C,但需注意这里需要是对应边之间的夹角),则三角形ABC是等腰三角形。不过需要注意的是,这里的判定更适用于证明两个三角形是否全等,而非直接判定一个三角形是否为等腰三角形。但在某些特定情境下,它也可以间接帮助我们得出结论。
判定定理2:角边角(ASA)
如果两个三角形有两角及它们之间的夹边相等,则这两个三角形全等。尽管这个定理同样更适用于证明两个三角形的全等,但在某些情况下,我们可以利用这个定理的逆过程来间接判定一个三角形是否为等腰三角形。例如,如果三角形ABC中已知∠A=∠B,且夹边AC(或AB)上的某条线段(如高、中线或角平分线)与∠C的某条性质(如角的平分线、垂直线等)符合等腰三角形的性质,则可以推断出三角形ABC是等腰三角形。
方法四:根据对称性质判定
等腰三角形具有对称性,这种对称性也可以用来判定一个三角形是否是等腰三角形。
对称性质
等腰三角形关于其底边中线所在的直线对称。如果三角形ABC关于某条直线l对称,且l是BC的中线,则三角形ABC是等腰三角形。
示例
设三角形ABC,直线l是BC的中线,且三角形ABC关于直线l对称。根据等腰三角形的对称性质,三角形ABC是等腰三角形。
方法五:通过构造辅助线判定
有时,我们可以通过构造辅助线来判定一个三角形是否是等腰三角形。
构造中线或高
如果三角形ABC中,我们可以构造BC的中线AD,或者BC边上的高AE,并证明AD(或AE)同时满足等腰三角形的其他性质(如三线合一),则三角形ABC是等腰三角形。
示例
设三角形ABC,构造BC的中线AD,并证明AD同时是BC边上的高和∠A的角平分线。根据等腰三角形的性质,三角形ABC是等腰三角形。
总结
等腰三角形的判定方法多种多样,包括根据定义判定、根据等腰三角形的性质判定、根据边角关系判定、根据对称性质判定以及通过构造辅助线判定。掌握这些方法,不仅能加深对等腰三角形性质的理解,还能在实际解题中灵活运用,提高解题效率。希望这篇文章能帮助大家更好地理解和掌握等腰三角形的判定方法。
- 上一篇: 如何访问手机百度云网盘登录页面
- 下一篇: 一键查询工商注册信息系统
-
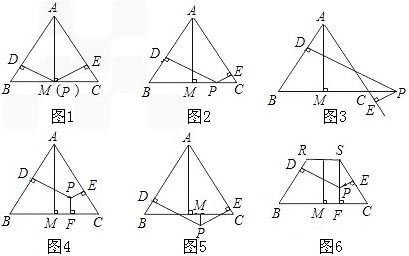
 六种全等三角形判定条件,你了解多少?资讯攻略12-06
六种全等三角形判定条件,你了解多少?资讯攻略12-06 -
 判定等边三角形的方法资讯攻略11-25
判定等边三角形的方法资讯攻略11-25 -
 揭秘等腰三角形的神秘定义资讯攻略03-01
揭秘等腰三角形的神秘定义资讯攻略03-01 -
 七巧板拼接技巧大揭秘资讯攻略11-26
七巧板拼接技巧大揭秘资讯攻略11-26 -
 **足球越位情况大揭秘:哪些情形属于越位?何时会被判越位?**资讯攻略11-13
**足球越位情况大揭秘:哪些情形属于越位?何时会被判越位?**资讯攻略11-13 -
 手作魅力大揭秘:轻松学会精致折纸花朵,让美在指尖绽放!资讯攻略10-27
手作魅力大揭秘:轻松学会精致折纸花朵,让美在指尖绽放!资讯攻略10-27












