六种全等三角形判定条件,你了解多少?
全等三角形是几何学中的一个重要概念,它指的是两个三角形在完全重合时,三边及三角均相等。在解决与三角形相关的问题时,判断两个三角形是否全等是至关重要的。为了系统地理解和应用全等三角形的判定条件,数学家们总结出了六种常用的判定方法。这些方法不仅具有理论价值,而且在解决实际问题时也非常实用。
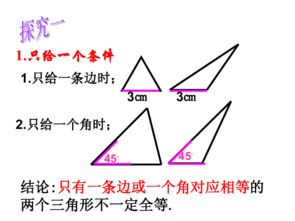
首先,第一种判定条件是SSS(Side-Side-Side)全等条件,即三边对应相等的两个三角形全等。这一判定条件的直观理解是,如果两个三角形的三条边分别相等,那么这两个三角形可以完全重合。在实际应用中,可以通过测量三角形的三边长度来判断它们是否全等。例如,在建筑设计中,工程师可能需要确保两个三角形结构件完全匹配,这时就可以利用SSS条件进行验证。

第二种判定条件是SAS(Side-Angle-Side)全等条件,指的是两边及它们之间的夹角对应相等的两个三角形全等。这一条件强调了夹角的重要性,即如果两个三角形的两边长度相等,且这两边之间的夹角也相等,那么这两个三角形就是全等的。SAS条件在几何证明中非常常见,因为它允许我们通过已知的两边和夹角来推断出三角形的其他性质。例如,在解决几何问题时,如果已知两个三角形的两边长度和夹角,就可以利用SAS条件来证明它们全等,从而进一步推导出其他相关的几何关系。

第三种判定条件是ASA(Angle-Side-Angle)全等条件,即两角及它们的夹边对应相等的两个三角形全等。ASA条件强调了角的重要性,它表明如果两个三角形的两个角分别相等,且这两个角之间的夹边也相等,那么这两个三角形就是全等的。这一判定条件在解决与角度相关的问题时特别有用。例如,在测量和绘图过程中,如果已知两个三角形的两个角和夹边长度,就可以利用ASA条件来验证它们的全等性,从而确保绘图的准确性。

第四种判定条件是AAS(Angle-Angle-Side)全等条件,指的是两角及非夹边对应相等的两个三角形全等。与ASA条件不同,AAS条件中的非夹边并不是两个相等角的直接夹边。然而,这一条件仍然有效,因为如果两个三角形的两个角分别相等,且这两个角所对的一条边也相等,那么这两个三角形就是全等的。AAS条件在解决某些特定类型的几何问题时非常有用,特别是当已知条件涉及到两个角和一条非夹边时。
第五种判定条件是HL(Hypotenuse-Leg)全等条件,这一条件仅适用于直角三角形。它指的是在直角三角形中,如果斜边和一条直角边对应相等,那么这两个直角三角形就是全等的。HL条件是基于直角三角形的特殊性质得出的,即直角三角形的斜边是确定其形状和大小的关键因素之一。因此,在解决与直角三角形相关的问题时,如果已知两个直角三角形的斜边和一条直角边长度相等,就可以利用HL条件来判断它们的全等性。
最后一种判定条件是RHS(Right-angle-Hypotenuse-Side)全等条件,虽然它并不如前面五种判定条件那样广为人知,但在某些情况下也非常有用。RHS条件指的是如果一个三角形是直角三角形,且它的斜边和一个锐角对应相等的两个三角形全等。这一条件实际上可以看作是HL条件的一种变体,因为它同样利用了直角三角形的斜边和角度信息来判断三角形的全等性。不过,与HL条件不同的是,RHS条件中的角度是锐角而不是直角边所对的角。
在实际应用中,这六种全等三角形的判定条件具有广泛的适用性。无论是在建筑设计、工程测量还是数学教育中,它们都是解决与三角形相关问题的有力工具。通过熟练掌握这些判定条件,我们可以更加准确地判断三角形的全等性,从而进一步推导出其他几何关系或解决实际问题。
例如,在建筑设计中,工程师可能需要确保两个三角形结构件能够完全匹配。这时,他们就可以利用SSS、SAS或ASA等判定条件来验证这两个三角形是否全等。如果验证结果表明它们全等,那么就可以确保结构件在安装过程中能够紧密配合,从而提高建筑的整体稳定性和安全性。
在工程测量中,全等三角形的判定条件同样发挥着重要作用。测量人员可以利用这些条件来验证测量结果的准确性。例如,在测量一个三角形的边长和角度时,他们可以利用SSS、SAS、ASA、AAS或HL等判定条件来判断测量结果是否一致。如果测量结果满足某个判定条件的要求,那么就可以认为测量结果是准确的。
此外,在数学教育中,全等三角形的判定条件也是重要的教学内容之一。通过学习和掌握这些判定条件,学生可以更好地理解三角形的性质和几何关系,从而提高他们的数学素养和解决问题的能力。
综上所述,全等三角形的六种判定条件在几何学中具有广泛的应用价值。它们不仅为我们提供了一种判断三角形全等性的有效方法,而且在解决实际问题时也发挥着重要作用。因此,在学习和研究几何学的过程中,我们应该深入理解和掌握这些判定条件,以便更好地应用它们来解决实际问题。
- 上一篇: iPhone 14有哪些颜色可选
- 下一篇: PS中如何实现羽化效果
-
 如何判断三角形全等的五种方法?资讯攻略01-18
如何判断三角形全等的五种方法?资讯攻略01-18 -
 等腰三角形判定技巧大揭秘资讯攻略02-25
等腰三角形判定技巧大揭秘资讯攻略02-25 -
 判定等边三角形的方法资讯攻略11-25
判定等边三角形的方法资讯攻略11-25 -
 揭秘等腰三角形的神秘定义资讯攻略03-01
揭秘等腰三角形的神秘定义资讯攻略03-01 -
 围棋获胜规则详解资讯攻略11-28
围棋获胜规则详解资讯攻略11-28 -
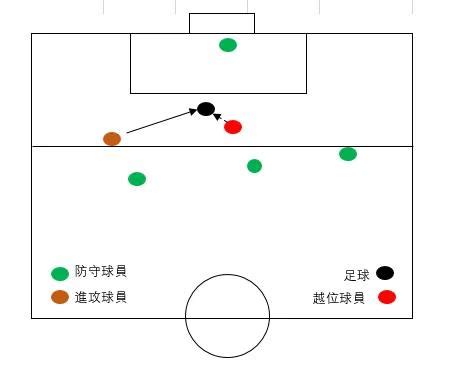 足球赛事中越位判定的解析资讯攻略11-22
足球赛事中越位判定的解析资讯攻略11-22












