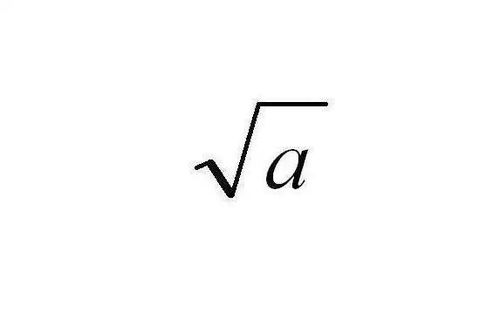如何快速用计算器算出一个数的平方根？

揭秘计算器如何高效求解平方根

在当今的数字时代，计算器已成为我们日常生活和学术研究中不可或缺的工具。无论是简单的加减乘除，还是复杂的科学计算，计算器都能迅速给出准确的结果。其中，计算一个数的平方根是计算器的一项基本功能。那么，计算器究竟是如何快速而准确地完成这一任务的呢？本文将从算法基础、硬件支持、软件实现及实际应用等多个维度进行深入剖析。

算法基础：牛顿迭代法与二分查找法

计算器求解平方根的核心在于其采用的算法。在众多算法中，牛顿迭代法和二分查找法因其高效性和稳定性而备受青睐。

牛顿迭代法

牛顿迭代法，又称牛顿-拉弗森方法，是一种在实数域和复数域上近似求解方程的方法。其基本思想是通过迭代逐步逼近方程的根。对于平方根问题，我们可以将其转化为求解方程$x^2 - a = 0$的根。牛顿迭代法的迭代公式为：

$x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}$

将$f(x) = x^2 - a$代入上式，得到：

$x_{n+1} = \frac{1}{2}(x_n + \frac{a}{x_n})$

选择一个合适的初始值$x_0$（通常选择被开方数a的一半或a本身作为初始值），通过不断迭代，我们可以得到一个逐渐逼近真实平方根的近似值。牛顿迭代法的收敛速度非常快，通常只需几次迭代就能达到很高的精度。

二分查找法

二分查找法是一种在有序数组中查找某一特定元素的搜索算法。虽然它最初是为数组搜索设计的，但经过适当改编，也可以用于求解平方根问题。对于给定的正数a，我们可以构造一个函数$f(x) = x^2 - a$，并在区间$[0, a]$（或$[0, \sqrt{a} \times 1.1]$等更精确的区间）上进行二分查找。通过不断缩小查找区间，我们可以找到一个满足$f(x) \approx 0$的x值，即a的平方根。二分查找法的优点是简单易懂，且能保证找到精确解（在给定精度范围内）。然而，与牛顿迭代法相比，其收敛速度较慢。

硬件支持：浮点运算单元与并行处理

计算器的快速计算能力不仅得益于高效的算法，还得益于其强大的硬件支持。其中，浮点运算单元（Floating Point Unit, FPU）和并行处理技术是提高计算器平方根计算速度的关键。

浮点运算单元

浮点运算单元是专门负责浮点算术运算的硬件组件。它支持包括加法、减法、乘法和除法在内的基本浮点运算，以及开方、指数和对数等特殊浮点运算。现代的FPU通常采用IEEE 754标准来表示和处理浮点数，该标准规定了浮点数的格式、精度和舍入规则等。通过高度集成的电路设计和优化的算法实现，FPU能够在极短的时间内完成复杂的浮点运算，包括平方根计算。

并行处理技术

并行处理技术允许计算器同时执行多个任务或运算步骤，从而显著提高计算速度。在计算平方根时，虽然单个迭代步骤可能无法直接并行化，但我们可以利用并行处理技术来加速迭代过程中的其他计算任务，如多次迭代之间的数据传递和存储访问等。此外，一些高级计算器或计算平台还支持向量化和SIMD（单指令多数据）指令集，这些技术能够进一步加速浮点运算的执行。

软件实现：编程语言与数学库

计算器的软件实现也是影响平方根计算速度的重要因素。不同的编程语言、编译器和数学库在性能和精度方面可能存在显著差异。

编程语言的选择

在选择编程语言时，我们需要权衡语言的表达力、执行效率和开发成本。对于平方根计算这样的数值计算任务，C和C等低级语言因其接近硬件的控制能力和高效的内存管理而备受青睐。然而，随着Python等高级语言的普及和NumPy等数学库的优化，使用高级语言进行数值计算也变得越来越可行和高效。

数学库的支持

数学库是提供数学函数和算法实现的软件组件。对于平方根计算，大多数编程语言的标准库或第三方数学库都提供了专门的函数或方法。例如，C语言中的`sqrt`函数、Python中的`math.sqrt`函数以及NumPy库中的`numpy.sqrt`函数等。这些函数通常基于高度优化的算法和硬件加速技术实现，能够在保证精度的同时提供极快的计算速度。

实际应用：科学计算与工程设计

计算器的平方根计算功能在多个领域具有广泛的应用价值。在科学计算和工程设计中，平方根运算常用于求解物理方程、进行数据分析、优化算法等。

科学计算

在科学计算中，平方根运算经常出现在各种物理公式和数学模型中。例如，在力学问题中求解速度、加速度和位移等物理量时，经常需要用到平方根运算。此外，在信号处理、图像处理、机器学习等领域中，平方根运算也扮演着重要角色。

工程设计

在工程设计领域，平方根运算同样具有广泛的应用。例如，在电路设计中计算电阻、电容和电感等元件的参数时，经常需要用到平方根运算。此外，在机械设计、航空航天、土木工程等领域中，平方根运算也常用于求解结构应力、变形和稳定性等问题。

结语

综上所述，计算器之所以能够快速而准确地计算一个数的平方根，得益于其采用的高效算法、强大的硬件支持、优化的软件实现以及广泛的应用场景。随着技术的不断发展，我们可以期待未来的计算器在平方根计算方面表现出更加出色的性能和精度。同时，我们也应该充分利用现有的技术和工具来解决实际问题，推动科学研究和工程设计的不断发展。