双曲线顶点坐标揭秘:直观图示带你秒懂!
双曲线的顶点坐标是指其在平面直角坐标系中的特殊点,这些点位于双曲线的两支曲线的交汇处,并且是双曲线上距离原点最近的点。在数学中,双曲线是一种常见的二次曲线,其标准方程和性质是研究其顶点坐标的基础。为了更好地理解双曲线的顶点坐标,我们可以通过图形来直观展示。
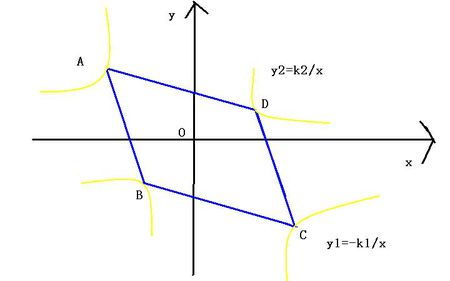
首先,我们回顾一下双曲线的标准方程。对于中心在原点的双曲线,如果其焦点位于x轴上,那么它的标准方程可以表示为:

x^2/a^2 - y^2/b^2 = 1
其中,a和b是常数,且a和b都大于0。这个方程描述了一个开口向右和向左的双曲线。如果焦点位于y轴上,标准方程则为:
y^2/a^2 - x^2/b^2 = 1
这时,双曲线开口向上和向下。
在这些标准方程中,a的值决定了双曲线的顶点坐标。对于x轴为焦轴的双曲线,其顶点坐标为(-a, 0)和(a, 0);对于y轴为焦轴的双曲线,顶点坐标为(0, -a)和(0, a)。这些顶点坐标是双曲线上最特别的点,因为它们不仅位于双曲线的两支曲线的交汇处,而且也是双曲线上距离原点最近的点。
为了更直观地理解这些概念,我们可以画一个双曲线的图。以下是一个简单的步骤说明,如何绘制一个以x轴为焦轴的双曲线图,并确定其顶点坐标。
第一步,选择一组a和b的值。为了简化,我们可以选择a=2和b=1。这些值决定了双曲线的形状和大小。
第二步,根据选择的a和b的值,写出双曲线的标准方程。在这个例子中,方程为:
x^2/4 - y^2/1 = 1
第三步,为了绘制双曲线,我们需要找到满足这个方程的点。这可以通过代入x的值并解出y的值来完成,反之亦然。由于双曲线是一个开放的曲线,我们无法绘制出所有的点,但可以通过绘制足够多的点来近似表示双曲线的形状。
第四步,选择一组x的值,并代入方程中求解y的值。例如,我们可以选择x=0, ±1, ±2, ±3等,并计算对应的y值。注意,由于方程中存在平方项,所以每个x值可能对应两个y值(一个正数和一个负数),除非x值正好是顶点坐标的x值(即±a)。
第五步,将计算出的点绘制在平面直角坐标系中。使用直线连接这些点,就可以得到一个近似的双曲线图。注意,由于双曲线是开放的,所以我们不需要连接所有的点,只需要连接那些能够清晰表示双曲线形状的点即可。
第六步,在绘制的双曲线图上,找到顶点坐标。在这个例子中,由于我们选择了a=2,所以顶点坐标为(-2, 0)和(2, 0)。这些点位于双曲线的两支曲线的交汇处,并且是双曲线上距离原点最近的点。
通过观察绘制的双曲线图,我们可以更直观地理解双曲线的顶点坐标。顶点坐标不仅是双曲线上的一个特殊点,而且它们还决定了双曲线的形状和位置。例如,如果我们改变a的值,那么顶点坐标就会改变,同时双曲线的形状和大小也会改变。同样地,如果我们改变b的值,双曲线的形状也会发生变化,但顶点坐标不会改变(除非我们也改变了a的值)。
除了通过绘制图形来理解双曲线的顶点坐标外,我们还可以通过分析双曲线的性质来进一步理解这些概念。例如,双曲线具有渐近线,这些渐近线是双曲线无限接近但永不相交的直线。对于以x轴为焦轴的双曲线,其渐近线方程为:
y = ±(b/a)x
这些渐近线通过原点,并且它们的斜率由a和b的比值决定。通过观察渐近线,我们可以更好地理解双曲线的开口方向和形状。同时,我们也可以注意到,顶点坐标位于渐近线的“拐点”处,即渐近线开始改变方向的地方。
此外,双曲线还具有对称性。对于以x轴为焦轴的双曲线,它关于x轴和原点对称;对于以y轴为焦轴的双曲线,它关于y轴和原点对称。这种对称性使得我们可以通过观察双曲线的一部分来推断出其整体形状和性质。
总的来说,双曲线的顶点坐标是其形状和位置的重要特征之一。通过绘制图形和分析性质,我们可以更好地理解这些概念,并掌握如何求解和应用它们。在实际应用中,双曲线的顶点坐标和性质在物理、工程、天文学等领域都有广泛的应用。例如,在物理学中,双曲线可以用来描述某些粒子的运动轨迹;在工程学中,双曲线可以用来设计某些结构的形状和尺寸;在天文学中,双曲线可以用来描述某些星系或星团的运动轨迹等。
- 上一篇: 马歇尔音箱怎么使用?
- 下一篇: 《诗》三百精髓,孔子一言蔽之:纯真无邪
-
 双曲线的顶点坐标公式及求解方法资讯攻略10-28
双曲线的顶点坐标公式及求解方法资讯攻略10-28 -
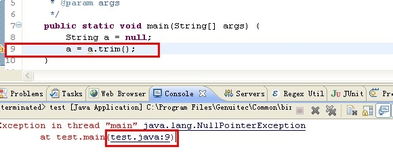 揭秘'null'的真正含义:一文带你秒懂!资讯攻略10-26
揭秘'null'的真正含义:一文带你秒懂!资讯攻略10-26 -
 深度解析:传动比是什么?一文带你秒懂!资讯攻略10-24
深度解析:传动比是什么?一文带你秒懂!资讯攻略10-24 -
 超简单!一问一答带你秒懂:如何快速建立微信群?资讯攻略10-27
超简单!一问一答带你秒懂:如何快速建立微信群?资讯攻略10-27 -
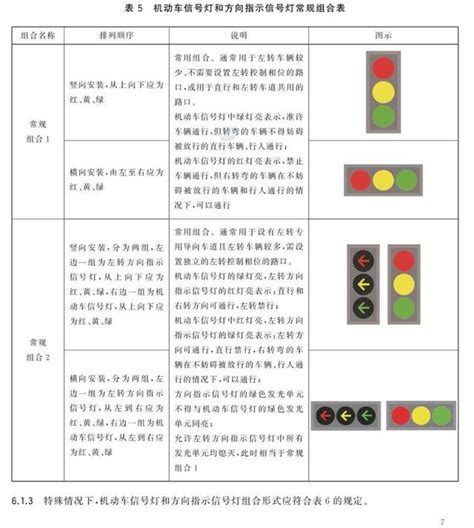 2024新版红绿灯来了,你真的会看吗?全面图解教你秒懂!资讯攻略12-04
2024新版红绿灯来了,你真的会看吗?全面图解教你秒懂!资讯攻略12-04 -
 揭秘:拐点究竟是指一个点还是坐标?资讯攻略12-02
揭秘:拐点究竟是指一个点还是坐标?资讯攻略12-02











