双曲线的顶点坐标公式及求解方法
双曲线顶点坐标,作为解析几何中一个重要的概念,是研究和理解双曲线性质的基础。在平面直角坐标系中,双曲线由两个分支组成,形状类似于两个无限延伸的弓形,而顶点坐标则是这两个分支与坐标轴的交点中最接近原点的位置。了解双曲线顶点坐标的计算方法和相关性质,有助于我们更深入地探索双曲线的几何特征和应用价值。

首先,我们来回顾一下双曲线的基本定义。双曲线是一种平面曲线,它由一个中心点和两个焦点组成,其中任一点到两个焦点的距离之差等于一个常数(且这个常数小于两焦点之间的距离)。在平面直角坐标系中,我们通常用标准方程来描述双曲线的形状和位置。根据焦点的位置,双曲线的标准方程有两种形式:一种是焦点在x轴上的双曲线方程,另一种是焦点在y轴上的双曲线方程。

对于焦点在x轴上的双曲线,其标准方程可以表示为:x^2/a^2 - y^2/b^2 = 1,其中a和b是常数,a代表双曲线与x轴的交点到原点的距离,b则与双曲线的宽度有关。在这个方程中,双曲线的顶点坐标即为(±a, 0)。也就是说,当y=0时,x的取值就是双曲线顶点的x坐标,而y坐标始终为0。这两个顶点分别位于x轴的正负两侧,是双曲线两个分支上最接近原点的点。

另一方面,对于焦点在y轴上的双曲线,其标准方程可以表示为:y^2/a^2 - x^2/b^2 = 1。同样地,a和b是常数,a代表双曲线与y轴的交点到原点的距离,b则与双曲线的宽度有关。在这个方程中,双曲线的顶点坐标变为(0, ±a)。也就是说,当x=0时,y的取值就是双曲线顶点的y坐标,而x坐标始终为0。这两个顶点分别位于y轴的正负两侧,同样是双曲线两个分支上最接近原点的点。

在计算双曲线顶点坐标时,我们需要注意以下几点:首先,要根据双曲线的标准方程确定焦点的位置(x轴或y轴);其次,要根据方程中的常数a来确定顶点到原点的距离;最后,根据焦点的位置和顶点到原点的距离,就可以准确地写出双曲线的顶点坐标。
除了顶点坐标外,双曲线还有其他一些重要的几何性质。例如,双曲线的渐近线方程。对于焦点在x轴上的双曲线,其渐近线方程为y = ±(b/a)x;对于焦点在y轴上的双曲线,其渐近线方程为y = ±(a/b)x。渐近线是双曲线的一种重要特征线,它描述了双曲线在无限远处的形状和走向。
此外,双曲线还有离心率这一重要性质。离心率e是双曲线的焦距c与实轴长2a之比,即e = c/a。离心率的大小反映了双曲线的开口程度和形状特征。当离心率e>1时,双曲线为开口型;当e越接近1时,双曲线的形状越接近椭圆;而当e越大时,双曲线的开口越宽。
在实际应用中,双曲线顶点坐标和相关性质具有广泛的应用价值。例如,在天文学中,我们可以利用双曲线的性质来描述某些天体的轨道运动;在物理学中,双曲线可以用于描述某些物理现象的边界条件;在工程学中,双曲线的形状和性质可以用于设计某些特殊的结构和设备。
此外,双曲线顶点坐标还在几何学、数学分析和计算机科学等领域中发挥着重要作用。在几何学中,我们可以利用双曲线的性质来解决一些与距离和角度相关的问题;在数学分析中,双曲线可以用于研究函数的极限和连续性等性质;在计算机科学中,双曲线的形状和性质可以用于图形渲染、图像处理和数据可视化等领域。
值得注意的是,虽然双曲线顶点坐标和相关性质在数学和物理学等领域中具有重要的应用价值,但在实际应用中我们也需要注意其局限性和适用范围。例如,在某些复杂情况下,双曲线的形状和性质可能会受到其他因素的影响而发生变化;此外,在计算和分析过程中我们也需要注意数据的准确性和精度问题。
总之,双曲线顶点坐标作为解析几何中一个重要的概念,具有广泛的应用价值和重要的理论意义。通过学习和掌握双曲线顶点坐标的计算方法和相关性质,我们可以更深入地了解双曲线的几何特征和应用价值,为数学、物理学和工程学等领域的研究和发展提供有力的支持。
在未来的学习和研究中,我们可以进一步探讨双曲线与其他几何图形之间的关系和联系,以及双曲线在更广泛领域中的应用和拓展。同时,我们也可以关注双曲线在新技术和新领域中的发展动态和趋势,为推动数学和物理学等领域的发展做出更大的贡献。
- 上一篇: 轻松上手:葫芦丝入门学习全教程
- 下一篇: 如何通过座机号码查询所属单位
-
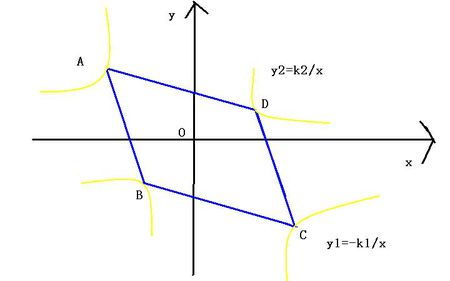 双曲线顶点坐标揭秘:直观图示带你秒懂!资讯攻略10-29
双曲线顶点坐标揭秘:直观图示带你秒懂!资讯攻略10-29 -
 顶点公式的具体表达是什么?资讯攻略12-03
顶点公式的具体表达是什么?资讯攻略12-03 -
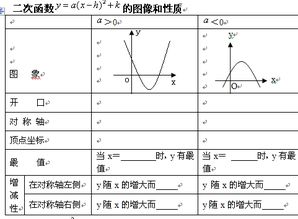 探索二次函数:图像之美与性质之谜资讯攻略11-08
探索二次函数:图像之美与性质之谜资讯攻略11-08 -
 什么是高等数学中的曲线拐点?如何求解拐点定义及方法资讯攻略11-24
什么是高等数学中的曲线拐点?如何求解拐点定义及方法资讯攻略11-24 -
 曲线积分的计算方法资讯攻略10-31
曲线积分的计算方法资讯攻略10-31 -
 如何求解轨迹方程的五种常用方法?资讯攻略12-01
如何求解轨迹方程的五种常用方法?资讯攻略12-01











