揭秘:卷积运算公式的奥秘与详解

在数字信号处理、图像处理和深度学习等领域,卷积运算无疑扮演着举足轻重的角色。这一数学工具不仅揭示了信号与系统之间的相互作用,还是构建卷积神经网络(CNN)这一深度学习领域的基石。那么,卷积运算公式究竟是什么呢?它背后的意义是什么?让我们一起揭开这个充满神秘色彩的数学公式,一窥其庐山真面目。
一、卷积运算的直观理解
在深入探究卷积运算公式之前,让我们先通过直观的方式理解卷积运算。想象一下,你手上有一个信号(或图像),这个信号可以是声音波形、股票价格序列或一张图片的像素值。现在,你想用一个“滤波器”对这个信号进行处理,以提取出某些特定的特征或去除噪声。这个滤波器本身也是一个信号,它的形状和大小决定了它如何影响原始信号。
卷积运算就是这样一个过程:你将滤波器在原始信号上滑动(或称之为“卷积”),在每个位置计算滤波器与原始信号重叠部分的乘积之和。这个过程不仅考虑了滤波器当前位置的信号值,还通过乘积和的方式融合了滤波器覆盖范围内的所有信号值。随着滤波器在原始信号上的滑动,你会得到一个新的信号,这个信号反映了原始信号经过滤波器处理后的特征。
二、卷积运算公式的数学表达
现在,让我们将上述直观理解转化为数学公式。卷积运算公式通常表示为:
y(t) = (x * h)(t) = ∫ x(τ)h(t - τ)dτ(连续情况)
或者
y[n] = (x * h)[n] = Σ x[k]h[n - k](离散情况)
其中,x 表示原始信号,h 表示滤波器(或称为核函数),y 表示经过卷积运算后的输出信号。在连续情况下,积分符号 ∫ 表示对时间变量 τ 进行积分;在离散情况下,Σ 表示对索引 k 进行求和。
三、公式中的关键要素
1. 时间变量:在连续情况下,时间变量 t 和 τ 分别表示当前时间和滤波器滑动到的时间位置;在离散情况下,n 和 k 分别表示信号的当前索引和滤波器滑动到的索引位置。
2. 乘积与求和:无论是连续情况还是离散情况,卷积运算都涉及两个信号的乘积和。在连续情况下,这是通过积分实现的;在离散情况下,这是通过求和实现的。
3. 滤波器翻转:值得注意的是,在原始的卷积定义中,滤波器 h 是需要翻转的(即 h(t - τ) 中的负号)。然而,在信号处理和深度学习领域,这种翻转通常被省略了,因为翻转与否并不改变卷积运算的本质特征。因此,在大多数情况下,我们可以直接使用 h(t - n) 或 h[n - k] 而不进行翻转。
四、卷积运算的意义与应用
卷积运算之所以在多个领域得到广泛应用,是因为它具有强大的特征提取和信号处理能力。以下是一些典型的应用场景:
1. 信号处理:在信号处理领域,卷积运算被用于滤波、去噪、特征提取等任务。例如,通过设计一个合适的滤波器,我们可以从声音信号中提取出语音特征,或者从地震信号中识别出地震波的类型。
2. 图像处理:在图像处理领域,卷积运算被用于边缘检测、模糊处理、图像增强等任务。通过设计不同的滤波器(如Sobel算子、Gaussian滤波器等),我们可以对图像进行各种处理操作。
3. 深度学习:在深度学习领域,卷积神经网络(CNN)是一种非常重要的模型结构。CNN通过多层卷积层、池化层和全连接层等结构,能够自动学习图像、语音等数据的特征表示,并在分类、检测、分割等任务中取得优异的性能。卷积层中的卷积运算正是CNN能够自动学习特征表示的关键所在。
五、卷积运算的计算与优化
在实际应用中,卷积运算的计算量可能非常大,特别是当处理大规模数据或复杂滤波器时。因此,如何高效地计算卷积运算成为了一个重要的问题。
1. 快速傅里叶变换(FFT):FFT是一种将时域信号转换为频域信号的算法,它可以在O(n log n)的时间复杂度内完成。通过FFT,我们可以将卷积运算转换为频域中的乘法运算,从而大大降低计算量。然而,FFT方法也有其局限性,如需要额外的内存来存储频域信号等。
2. 稀疏卷积:在深度学习领域,为了降低卷积运算的计算量,研究者们提出了稀疏卷积的概念。稀疏卷积通过减少滤波器中零元素的数量来降低计算密度,从而在不牺牲性能的情况下提高计算效率。
3. 深度可分离卷积:深度可
- 上一篇: 在家如何制作凉粉?
- 下一篇: 微信实名认证全攻略:轻松几步完成认证!
-
 揭秘幂的运算法则:掌握数学中的指数奥秘资讯攻略10-30
揭秘幂的运算法则:掌握数学中的指数奥秘资讯攻略10-30 -
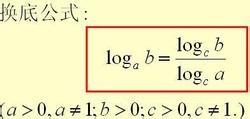 对数基本公式:详解log函数的定义与应用资讯攻略10-26
对数基本公式:详解log函数的定义与应用资讯攻略10-26 -
 揭秘:电势差公式的奥秘与应用资讯攻略10-31
揭秘:电势差公式的奥秘与应用资讯攻略10-31 -
 Excel中如何进行乘法运算的函数公式资讯攻略12-03
Excel中如何进行乘法运算的函数公式资讯攻略12-03 -
 掌握对数运算的核心公式,轻松解题无烦恼资讯攻略10-27
掌握对数运算的核心公式,轻松解题无烦恼资讯攻略10-27 -
 Excel乘法运算公式大全资讯攻略11-20
Excel乘法运算公式大全资讯攻略11-20