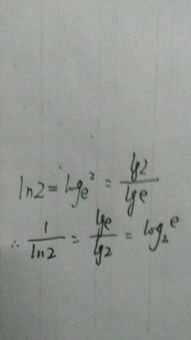对数基本公式:详解log函数的定义与应用
在数学的浩瀚宇宙中,对数(Logarithm)这一概念犹如一颗璀璨的星辰,它不仅照亮了算术与代数的边界,还在科学、工程乃至日常生活中发挥着不可替代的作用。对于初涉数学殿堂或是渴望深化知识理解的探索者来说,掌握对数的基本公式无疑是打开这扇奇妙大门的关键钥匙。那么,就让我们一同踏上这段探索之旅,揭开“log对数基本公式”的神秘面纱。
对数的起源与定义
故事始于17世纪,苏格兰工程师约翰·纳皮尔在解决天文学计算中复杂乘法问题时,创造性地发明了“对数”这一工具。对数,简而言之,是一种将乘除运算转化为加减运算的数学手段,极大地简化了复杂数值的计算过程。其基本定义建立在指数关系之上:如果`a^x = N`(其中`a`是底数,`x`是对数,`N`是真数,且`a > 0`,`a ≠ 1`),那么数`x`就是以`a`为底`N`的对数,记作`x = log_a(N)`。

对数的基本公式
1. 对数的换底公式
在探索对数的世界中,换底公式是一把万能钥匙,它允许我们在不同的对数系统间自由转换。公式表达为:

\[
\log_b(N) = \frac{\log_a(N)}{\log_a(b)}
\]
这里,`a`和`b`可以是任何正数且不等于1,`N`是正数。换底公式的价值在于,它使得我们可以利用已知的对数(如自然对数`ln`或常用对数`log`)来计算其他底数的对数。
2. 对数的乘法法则
当需要计算两个数乘积的对数时,乘法法则为我们提供了便捷的途径:
\[
\log_a(M \cdot N) = \log_a(M) + \log_a(N)
\]
这一法则直接体现了对数将乘法转化为加法的特性,极大地简化了计算过程。
3. 对数的除法法则
与乘法法则相对应,当遇到除法运算时,对数同样有其独特的简化方式:
\[
\log_a\left(\frac{M}{N}\right) = \log_a(M) - \log_a(N)
\]
这里需要注意的是,`N`不能为0,因为对数函数的定义域要求真数必须为正数。
4. 对数的幂运算法则
在处理数的幂的对数时,我们有:
\[
\log_a(M^n) = n \cdot \log_a(M)
\]
这一公式表明,一个数的幂的对数等于该数的对数与幂指数的乘积,它再次展示了对数在简化复杂运算中的强大能力。
应用实例
理解了这些基本公式后,我们不妨通过一个简单的例子来看看它们是如何在实际问题中发挥作用的。假设我们需要计算`81`的平方根,利用对数的性质,我们可以这样操作:
首先,注意到`81`的平方根是`9`,因为`9^2 = 81`。如果我们想利用对数来求解,可以将其转化为对数方程:
\[
\sqrt{81} = 81^{\frac{1}{2}}
\]
然后,应用对数的幂运算法则:
\[
\log_a(81^{\frac{1}{2}}) = \frac{1}{2} \log_a(81)
\]
这里,我们假设使用以10为底的常用对数(即`log`,通常省略底数表示以10为底),则:
\[
\log(\sqrt{81}) = \frac{1}{2} \log(81)
\]
由于`log(81) ≈ 1.9085`(近似值),所以:
\[
\log(\sqrt{81}) \approx \frac{1}{2} \times 1.9085 \approx 0.9543
\]
但记住,我们的目标不是找到对数的值,而是找到原数。因此,我们需要将对数值转换回原数。由于`log(9) ≈ 0.9543`,我们可以推断出`81`的平方根是`9`。
当然,这个例子略显复杂且略显多余(因为直接开方更为直接),但它生动地展示了如何通过对数来间接解决问题,尤其是在处理更复杂或需要特定对数转换的问题时,这种方法尤为重要。
结语
至此,我们已初步领略了“log对数基本
-
 揭秘:log函数的定义域究竟隐藏着什么奥秘?资讯攻略11-23
揭秘:log函数的定义域究竟隐藏着什么奥秘?资讯攻略11-23 -
 掌握log函数求导公式,轻松解决数学问题资讯攻略11-09
掌握log函数求导公式,轻松解决数学问题资讯攻略11-09 -
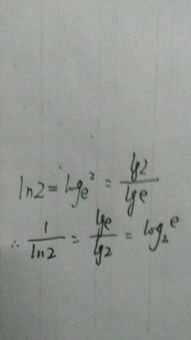 揭秘:log2到底是什么?一文读懂!资讯攻略11-10
揭秘:log2到底是什么?一文读懂!资讯攻略11-10 -
 探索对数函数导数的奥秘资讯攻略11-04
探索对数函数导数的奥秘资讯攻略11-04 -
 指数函数有哪8个基本公式?资讯攻略11-21
指数函数有哪8个基本公式?资讯攻略11-21 -
 高中数学必备:三角函数公式全集(终极版)资讯攻略11-30
高中数学必备:三角函数公式全集(终极版)资讯攻略11-30