标准差公式是什么?
标准差公式是统计学中一个至关重要的概念,用于衡量数据集的离散程度。通过计算标准差,我们可以了解数据点围绕平均值的分布情况,从而评估数据的波动性和一致性。本文将详细介绍标准差公式的原理、计算方法及其在数据分析中的应用,旨在帮助读者深入理解这一重要工具。
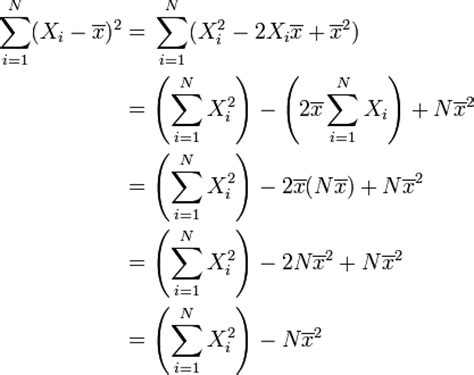
首先,标准差的核心在于描述数据集的变异程度。一个数据集中的各个数值可能围绕平均值分布,而这些数值与平均值的偏差(即离差)可以反映数据的波动情况。标准差正是这些离差平方的平均值的平方根,因此也被称为均方误差的平方根。其计算公式为:σ = √[(Σ(x - μ)^2) / N],其中σ表示标准差,x为数据集中的每一个数值,μ为平均值,N为数据点的总数。

在了解公式本身之前,我们首先需要计算数据集的平均值(μ)。平均值是所有数据点的总和除以数据点的总数,即μ = (Σx) / N。这一步骤是计算标准差的基础,因为标准差是基于数据点与平均值的偏差来计算的。

接下来,我们逐一分析标准差公式中的各个组成部分。公式中的(x - μ)表示每个数据点与平均值的偏差。通过计算每个数据点的偏差,我们可以了解每个数据点距离平均值的距离。然而,直接计算这些偏差的平均值可能会受到正负偏差相互抵消的影响,从而低估数据的波动程度。因此,标准差公式中采用了偏差的平方((x - μ)^2),以确保所有的偏差都被正向考虑,不会因为正负相消而减弱波动性的表现。

在计算了每个数据点偏差的平方后,我们将这些平方值相加,并除以数据点的总数(N),得到偏差平方的平均值。这一步骤是计算标准差公式的分子部分。最终,我们取这个平均值的平方根,即得到标准差σ。通过平方根运算,标准差保留了原始数据的单位,使得标准差的值在量纲上与原始数据一致,便于理解和比较。

标准差的应用非常广泛,尤其在数据分析、科学研究、金融投资等领域。在数据分析中,标准差可以帮助我们识别数据中的异常值。如果一个数据点的偏差远超过标准差的范围,那么它可能是一个异常值或错误数据,需要进一步检查和处理。此外,标准差还可以用于比较不同数据集的离散程度。当两个数据集的平均值相近时,标准差较大的数据集意味着其数据点更加分散,而标准差较小的数据集则更加集中。
在科学研究中,标准差也是评估实验结果稳定性和重复性的重要指标。通过计算实验数据的标准差,研究人员可以了解实验结果的波动性,从而评估实验的可靠性和准确性。在金融投资领域,标准差被广泛应用于风险分析。投资组合的标准差可以反映其收益率的波动性,进而评估投资风险。投资者通常会选择标准差较小的投资组合,以降低投资风险并提高收益的稳定性。
除了基本的标准差外,还有一个与之相关的概念是样本标准差。在实际应用中,我们往往无法获取到总体数据的全部信息,而只能通过分析样本数据来推断总体的特性。因此,在计算标准差时,我们需要考虑样本数据的特点。样本标准差的计算公式与总体标准差类似,但在分母部分有所不同。样本标准差的分母是N-1(即样本数减1),而不是N。这一调整是为了纠正样本数据带来的偏差,使得样本标准差的计算结果更加接近总体标准差。
在实际操作中,计算标准差时需要注意几个关键点。首先,要确保数据集的完整性和准确性,避免遗漏或错误的数据点影响计算结果。其次,在计算平均值时,要确保所有数据点都被平等地考虑,避免出现偏差。最后,在计算标准差时,要正确应用公式,特别是要注意分母部分的取值。
总之,标准差公式是统计学中一个重要的工具,用于衡量数据集的离散程度。通过计算标准差,我们可以了解数据点围绕平均值的分布情况,从而评估数据的波动性和一致性。标准差在数据分析、科学研究、金融投资等领域具有广泛的应用价值,可以帮助我们识别异常值、比较数据集的离散程度、评估实验结果的稳定性和重复性、分析投资风险等。因此,掌握标准差公式的原理和应用方法对于提高数据分析能力和科学研究水平具有重要意义。
最后,需要强调的是,标准差只是衡量数据离散程度的一种方法,它并不能完全反映数据的所有特征。在实际应用中,我们还需要结合其他统计指标和方法来全面分析数据。同时,对于不同类型的数据和场景,可能需要采用不同的统计方法和模型来进行分析和预测。因此,在进行数据分析时,我们应该保持开放和灵活的态度,不断探索和尝试新的方法和工具,以提高数据分析和决策的科学性和准确性。
- 上一篇: 如何在京东上打开小金库?
- 下一篇: 小米手机如何设置地震提醒功能?
-
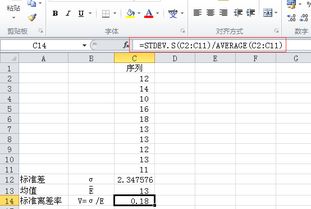 如何在Excel中使用标准差公式函数?资讯攻略12-03
如何在Excel中使用标准差公式函数?资讯攻略12-03 -
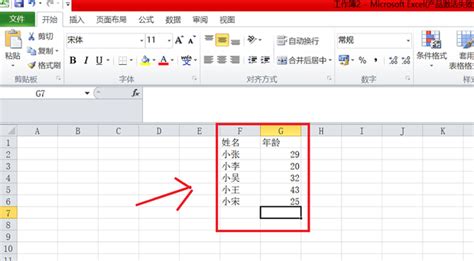 如何在Excel中轻松计算标准差?资讯攻略11-22
如何在Excel中轻松计算标准差?资讯攻略11-22 -
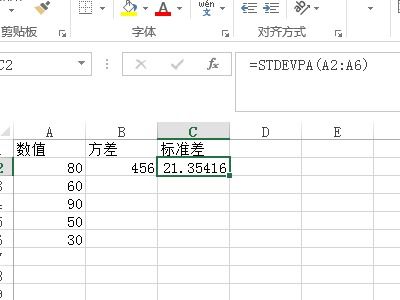 揭秘:计算器如何轻松搞定方差与标准差计算资讯攻略10-30
揭秘:计算器如何轻松搞定方差与标准差计算资讯攻略10-30 -
 如何在Excel中使用标准差函数?资讯攻略11-22
如何在Excel中使用标准差函数?资讯攻略11-22 -
 如何在Excel中计算标准差?资讯攻略11-24
如何在Excel中计算标准差?资讯攻略11-24 -
 Excel中标准差计算的实用教程资讯攻略11-23
Excel中标准差计算的实用教程资讯攻略11-23











