揭秘!棱锥的多种分类,你了解几种?
棱锥,这一几何形体,以其独特的结构美和广泛的应用性,在数学、建筑、艺术等多个领域占据着重要位置。它由一个多边形底面以及与之相连并交于一点的多个三角形侧面所构成,这种简单的几何构造背后,隐藏着丰富的分类与变化。今天,我们就一同探索棱锥世界的奥秘,了解它究竟可以划分为哪几种不同的类型。
一、基础分类:按底面边数划分
棱锥最直观也最基本的分类方式,便是根据其底面的边数来划分。底面边数的不同,决定了棱锥的形状、侧面数以及顶点的连接方式的多样性。
1. 三棱锥(四面体):底面为三角形的棱锥,是棱锥中最基础也最常见的一种。它拥有四个面(三个侧面加一个底面),六条棱,以及四个顶点。三棱锥的稳定性极好,是构成许多复杂结构的基本单元,如金字塔的塔身便是三棱锥形状的典型应用。
2. 四棱锥:底面为四边形的棱锥。根据四边形底面是否规则(如矩形、正方形、梯形或不规则四边形),四棱锥的形态也会有所变化。四棱锥共有五个面,八条棱,五个顶点。在建筑设计中,四棱锥形态常被用于创造独特的视觉效果,如屋顶结构或装饰元素。
3. 五棱锥及以上:随着底面边数的增加,棱锥的复杂度也随之上升。五棱锥、六棱锥……乃至n棱锥(n为多边形的边数),它们各自拥有更多的面、棱和顶点。这些棱锥在几何学研究中占有重要地位,同时也是艺术创作中探索形态与空间关系的灵感源泉。
二、特殊类型:基于性质与应用的细分
除了按底面边数进行的基础分类外,棱锥还可以根据其他特性或应用场景进行更细致的划分。
1. 直棱锥与斜棱锥:这是根据棱锥顶点到底面所在平面的垂直关系来区分的。直棱锥的顶点与底面各顶点连线均垂直于底面,而斜棱锥则至少有一条侧棱不垂直于底面。直棱锥在几何计算中更为简便,而斜棱锥则展现了更为复杂多变的空间形态。
2. 正棱锥:当棱锥的底面是正多边形,且顶点到底面的投影是底面的中心时,这样的棱锥被称为正棱锥。正棱锥的侧面均为全等的等腰三角形,具有高度的对称性和美感,是几何学和建筑学中的宠儿。
3. 等边等面积棱锥:虽然不常见,但理论上存在一种棱锥,其所有侧面不仅全等,而且面积也相等。这种棱锥的底面通常为一种特殊形状的多边形,顶点位置需精确计算以确保侧面的等面积特性。
4. 应用中的棱锥:在实际应用中,棱锥的身影无处不在。从古代的角锥体建筑(如埃及金字塔),到现代的桥梁支撑结构、航天器的天线设计,甚至是微观世界中的分子构型,棱锥及其变体都发挥着关键作用。这些应用不仅体现了棱锥结构的稳定性和承载力,也展现了人类对其美学价值的追求。
三、结语
棱锥,这一看似简单的几何形体,实则蕴含了丰富的分类与变化。从基础的三棱锥到复杂的n棱锥,从直棱锥到斜棱锥,再到正棱锥等特殊类型,每一种棱锥都以其独特的形态和性质,在几何学、建筑学、艺术乃至更广泛的领域中扮演着重要角色。通过对棱锥分类的深入探索,我们不仅能够更好地理解这一几何形态的多样性和美感,也能在实际应用中更加灵活地运用它们,创造出更加丰富多彩的空间形态和视觉体验。
- 上一篇: 油菜花通常在什么时候盛开?
- 下一篇: 高中物理中如何直接判断比结合能的大小
-
 盐的多种分类方法,你了解多少?资讯攻略12-07
盐的多种分类方法,你了解多少?资讯攻略12-07 -
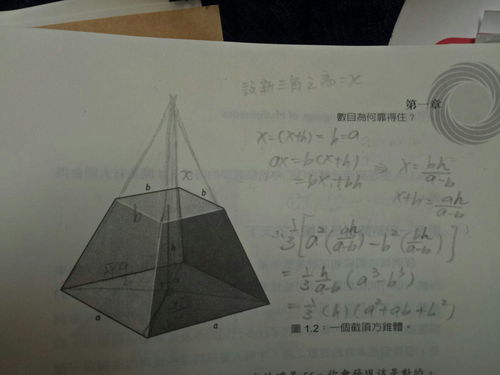 棱锥体积公式详解,轻松掌握!资讯攻略10-30
棱锥体积公式详解,轻松掌握!资讯攻略10-30 -
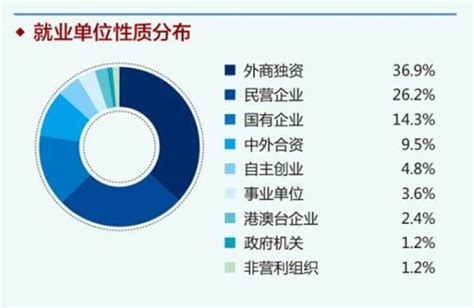 揭秘:单位性质与经济类型的多样化分类详解资讯攻略02-17
揭秘:单位性质与经济类型的多样化分类详解资讯攻略02-17 -
 揭秘动物王国的分类奥秘资讯攻略11-05
揭秘动物王国的分类奥秘资讯攻略11-05 -
 动物的分类方法通常有几种?资讯攻略11-04
动物的分类方法通常有几种?资讯攻略11-04 -
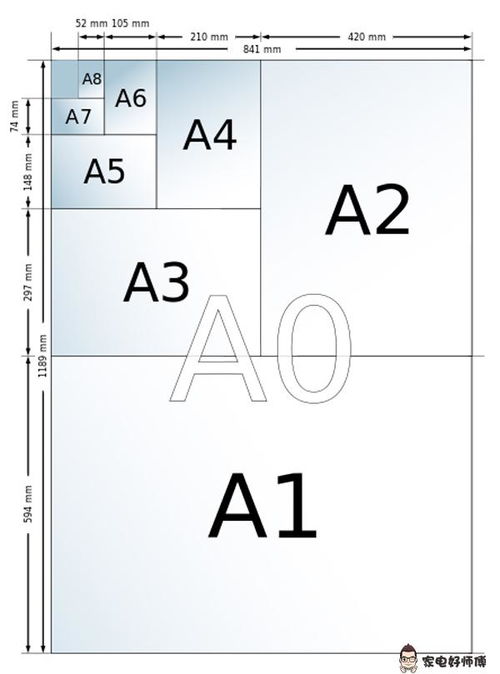 揭秘!日常生活中最常用的纸张尺寸有哪些?资讯攻略11-01
揭秘!日常生活中最常用的纸张尺寸有哪些?资讯攻略11-01












