棱锥体积公式详解，轻松掌握！

棱锥的体积公式是几何学中的一个重要内容，它帮助我们计算三维空间中具有特定形状物体的体积。这个公式不仅在数学课程中占据重要地位，还在工程、建筑设计以及物理科学等多个领域有着广泛的应用。本文将从棱锥的定义、体积公式的推导、公式的应用以及与其他几何体的关系等多个维度，详细探讨棱锥的体积公式。

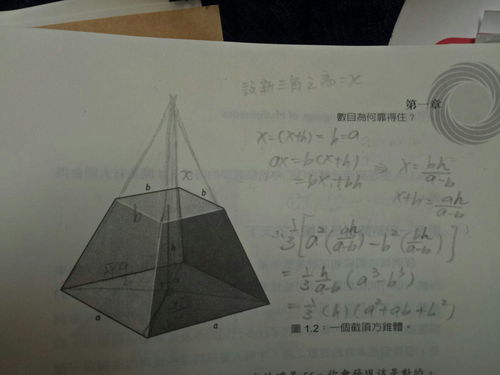
一、棱锥的定义

棱锥是一种多面体，它由一个多边形底面及与其各顶点相连的三角形侧面组成。底面可以是任意多边形，如三角形、四边形、五边形等，而侧面则始终是三角形。根据底面的形状，棱锥可以分为不同的类型，如三棱锥（底面为三角形）、四棱锥（底面为四边形）等。在所有棱锥中，最常见且最简单的是三棱锥，也称为四面体。

棱锥有一个独特的性质，即所有侧面三角形的顶点都位于同一条直线上，这条直线被称为棱锥的高。高是从底面到顶点的垂直距离，它在计算棱锥体积时起着关键作用。

二、棱锥体积公式的推导

棱锥体积的计算公式是：

\[V = \frac{1}{3} \times \text{底面积} \times \text{高}\]

这个公式看似简单，但其背后的推导过程却充满了数学智慧。

首先，我们可以从特殊的三棱锥（四面体）开始推导。假设有一个三棱锥，其底面为三角形ABC，顶点为D，高为h（从D垂直于底面ABC的垂线）。

为了简化问题，我们可以设想一个与三棱锥底面ABC平行且距离为h的平面，然后在这个平面上作一个与底面ABC全等的三角形A'B'C'。这样，我们就构造出了一个与三棱锥等高的平行六面体ABCD-A'B'C'D'（其中D'是垂足，与D相对）。

接下来，我们将三棱锥分解为三个小四面体：三棱锥D-ABA'、三棱锥D-BCA'和三棱锥D-CCA'。注意到，这三个小四面体的高都是h，底面分别是三角形ABA'、三角形BCA'和三角形CCA'（这些三角形都是平行四边形的一半，因此面积与三角形ABC相等）。

由于平行六面体的体积可以通过底面积乘以高来计算（即V_{\text{平行六面体}} = \text{底面积} \times h），并且这个体积等于三个小四面体体积之和，我们可以得到：

\[V_{\text{平行六面体}} = V_{\text{D-ABA'}} + V_{\text{D-BCA'}} + V_{\text{D-CCA'}}\]

由于每个小四面体的底面积都与三角形ABC相等，我们可以将每个小四面体的体积表示为：

\[V_{\text{D-ABA'}} = \frac{1}{3} \times \text{面积(ABA')} \times h = \frac{1}{3} \times \text{面积(ABC)} \times h\]

同理，其他两个小四面体的体积也是这样的表达式。因此，平行六面体的体积为：

\[V_{\text{平行六面体}} = 3 \times \frac{1}{3} \times \text{面积(ABC)} \times h = \text{面积(ABC)} \times h\]

现在，我们回到原始的三棱锥D-ABC。由于它是平行六面体体积的三分之一（因为我们只考虑了三个小四面体中的一个），我们可以得出三棱锥的体积公式：

\[V_{\text{D-ABC}} = \frac{1}{3} \times \text{面积(ABC)} \times h\]

这个推导过程可以推广到任意棱锥，因为任意棱锥都可以通过类似的方式分解为一系列小的四面体，并且这些四面体的体积之和等于一个与棱锥等高的平行多面体的体积。由于平行多面体的体积是底面积乘以高，而棱锥的体积是这个体积的三分之一，因此棱锥的体积公式就得到了证明。

三、棱锥体积公式的应用

棱锥体积公式在工程、建筑设计以及物理科学中有着广泛的应用。以下是一些具体例子：

1. 工程设计：在土木工程中，棱锥形状的结构（如屋顶、塔尖等）很常见。设计师需要知道这些结构的体积，以便进行材料计算和成本估算。棱锥体积公式为此提供了便捷的工具。

2. 建筑设计：在建筑设计中，棱锥形状的元素（如装饰性雕塑、照明装置等）可能用于增加建筑的艺术感和功能性。通过计算这些元素的体积，设计师可以更好地理解它们的空间占用情况，从而优化布局和视觉效果。

3. 物理科学：在物理学中，棱锥形状的天线、探测器等元件常用于电磁波的传播和接收。了解这些元件的体积有助于科学家进行性能分析和优化设计。此外，在地质学和水文学中