如何计算地球的角速度和线速度?求公式详解
在浩瀚的宇宙中,地球以它那独特而优雅的姿态缓缓旋转,不仅带给我们昼夜交替的奇妙体验,还孕育了万物生灵。今天,我们不谈那些宏大的宇宙哲学,而是深入探索一个既基础又引人入胜的话题——地球的角速度与线速度,以及它们背后那些简单却神奇的计算公式。让我们一同揭开这层神秘的面纱,用简单易懂的语言,带你领略地球旋转的奥秘。

地球的自转:角速度与线速度的舞蹈
首先,让我们从地球的自转说起。想象一下,如果你站在地球的极点,你会看到整个世界如同一个巨大的陀螺,在不断地旋转着。这种旋转,就是地球的自转。而描述这种旋转快慢的方式,主要有两种:角速度和线速度。

角速度,顾名思义,就是单位时间内物体绕圆心转过的角度。对于地球自转而言,角速度可以简单理解为地球每小时转过的度数。通过计算,我们得知地球自转一周(360度)大约需要23小时56分4秒,这个时间也被称为恒星日。因此,地球的角速度就是360度除以这个时间,结果大约是15度/小时。这个数字,就像是地球自转速度的一个“节拍器”,稳定而规律地推动着日夜的更迭。

然而,仅仅知道角速度还不足以完全描绘地球自转的壮观景象。我们还需要了解另一个重要的概念——线速度。线速度,指的是物体在圆周运动中,沿其运动轨迹单位时间所经过的距离。对于地球上的每一点来说,由于其到地球旋转轴(即地轴)的距离不同,其线速度也会有所差异。
线速度的计算:从赤道到极点的奇妙变化
要计算地球上某点的线速度,我们需要用到一个简单的公式:线速度 = 角速度 × 转动半径。这里的转动半径,对于地球来说,就是该点到地轴的垂直距离。由于地球是一个椭球体,赤道半径略大于极半径,因此赤道上的线速度是最大的。
具体来说,赤道上的线速度可以通过将地球的角速度(15度/小时,换算成弧度制为π/12弧度/小时,因为1度约等于π/180弧度)乘以赤道的半径(约为6378千米)来得到。计算后,我们得知赤道上的线速度约为1670千米/小时。这个数字意味着,在赤道上,你即使原地不动,也能以这样的速度“飞驰”过地球的表面。
然而,随着纬度的增加,转动半径逐渐减小,线速度也随之降低。例如,在南北纬30度的地方,线速度约为1447千米/小时;而在南北纬60度的地方,则降低到了837千米/小时。最终,在地球的极点,由于转动半径为零,因此线速度也降为零,即极点没有线速度。
公式背后的奥秘:从理论到实践
上述的角速度和线速度计算公式,看似简单,却蕴含着丰富的物理原理和宇宙法则。它们不仅是我们理解地球自转的基础,也是研究天体运动、宇宙航行等领域的重要工具。
角速度公式ω=Ч/t(Ч为所走过弧度,t为时间)和线速度公式v=ω*r(v为线速度,ω为角速度,r为转动半径),这两个公式紧密相连,共同揭示了物体在圆周运动中的基本规律。在地球自转这个具体的例子中,我们可以看到,随着转动半径r的变化,线速度v也相应地发生变化,而角速度ω则保持不变(在忽略地球自转速度微小变化的情况下)。
探索的乐趣:从日常到宇宙
了解了地球的角速度和线速度之后,你会发现这些看似抽象的概念其实与我们的日常生活息息相关。比如,为什么赤道地区的气候通常比极地地区更加炎热?这在一定程度上与赤道地区的线速度较大、接收到的太阳辐射更多有关。再比如,当我们乘坐飞机从赤道飞向极地时,会感受到飞机速度的变化,这背后也隐藏着线速度差异的秘密。
更进一步地,对地球角速度和线速度的研究,还帮助我们理解了更多关于宇宙中天体运动的奥秘。从月球绕地球的旋转,到行星绕太阳的公转,再到整个银河系乃至宇宙的演化,角速度和线速度都是不可或缺的基本概念。
结语
地球的自转,是一场永不停歇的舞蹈,而角速度和线速度则是这场舞蹈的节拍和旋律。通过简单的计算公式,我们不仅能够量化这场舞蹈的速度和节奏,还能深入探索其背后的物理原理和宇宙法则。希望这篇文章能够激发你对地球自转乃至整个宇宙的好奇心和探索欲,让我们一起在知识的海洋中遨游,发现更多未知的奥秘。
-
 六大相遇问题核心公式详解资讯攻略10-26
六大相遇问题核心公式详解资讯攻略10-26 -
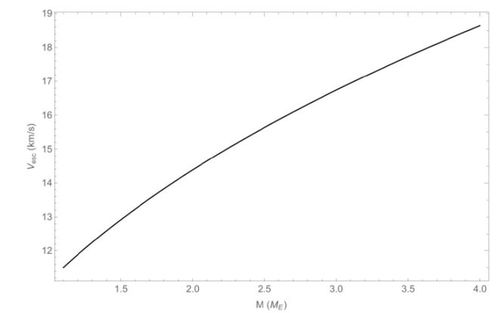 揭秘:如何精准计算逃逸速度?资讯攻略11-04
揭秘:如何精准计算逃逸速度?资讯攻略11-04 -
 揭秘:第一宇宙速度究竟是多少?资讯攻略10-27
揭秘:第一宇宙速度究竟是多少?资讯攻略10-27 -
 如何区分:平均速度、平均速率、瞬时速度与瞬时速率资讯攻略11-13
如何区分:平均速度、平均速率、瞬时速度与瞬时速率资讯攻略11-13 -
 揭秘:增速计算公式的奥秘与应用资讯攻略11-06
揭秘:增速计算公式的奥秘与应用资讯攻略11-06 -
 如何计算带传动的传动比?资讯攻略10-25
如何计算带传动的传动比?资讯攻略10-25












