怎样把十进制数转换成二进制形式?
当我们深入探索数字世界的奥秘时,理解不同数制之间的转换是至关重要的。在众多数制中,二进制与十进制因其各自独特的特性和广泛应用而备受关注。二进制,作为计算机内部信息存储与处理的基石,其简洁性和直接性使得计算机操作变得高效而可靠。而十进制,作为我们日常生活中最常用的数制,其直观易懂的特点深入人心。那么,如何从我们熟悉的十进制转换到二进制呢?本文将从原理解析、手动转换方法、快速转换技巧以及实际应用等多个维度,详细阐述这一转换过程。

一、原理解析:十进制与二进制的本质区别
1.1 十进制基础
十进制,即逢十进一,是基于10个基本符号(0-9)的计数系统。在十进制中,每一位数字代表的权值是该位所处的位置乘以10的幂次方(从右至左,个位为10^0,十位为10^1,以此类推)。例如,数字234中,2代表200(即2*10^2),3代表30(即3*10^1),4代表4(即4*10^0),三者相加得到234。

1.2 二进制简介
二进制,则是一种仅包含两个基本符号(0和1)的数制,遵循逢二进一的原则。在二进制中,每一位数字代表的权值是该位所处的位置乘以2的幂次方(同样从右至左,最低位为2^0,次低位为2^1,依此类推)。例如,二进制数101中,最右边的1代表1(即1*2^0),中间的0不贡献值,最左边的1代表4(即1*2^2),三者相加得到5,即二进制数101对应的十进制数为5。

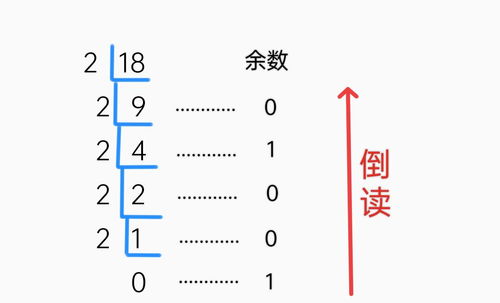
二、手动转换方法:除2取余法
将十进制数转换为二进制数,最常用的方法是“除2取余法”。该方法简单直观,步骤如下:
1. 将被转换的十进制数除以2:记录余数,这是二进制数的一位。
2. 将得到的商再次除以2:继续记录余数,直至商为0。
3. 将所有余数按逆序排列:即最先得到的余数放在最低位,最后得到的余数放在最高位,这就是对应的二进制数。
示例
将十进制数23转换为二进制数:
1. 23 ÷ 2 = 11 ... 余 1 → 记录1
2. 11 ÷ 2 = 5 ... 余 1 → 记录1
3. 5 ÷ 2 = 2 ... 余 1 → 记录1
4. 2 ÷ 2 = 1 ... 余 0 → 记录0
5. 1 ÷ 2 = 0 ... 余 1 → 记录1
逆序排列余数得:10111,所以23的二进制表示为10111。
三、快速转换技巧
虽然除2取余法是转换的基础,但在处理较大数或需要快速转换时,掌握一些技巧可以大大提高效率。
3.1 记忆常见数的二进制表示
熟记一些常用的十进制数(如2的幂次方)的二进制表示,可以在转换时直接引用,减少计算量。
3.2 利用位操作(针对编程)
在编程中,可以利用位移(左移<<、右移>>)和位与(&)等位操作来快速实现十进制到二进制的转换,尤其是在处理整数时效率极高。
3.3 分段转换
对于非常大的数,可以将其拆分成较小的段分别进行转换,然后再合并结果。这种方法可以降低一次性处理的难度,同时保持转换的准确性。
四、实际应用:二进制在计算机科学中的重要性
二进制不仅是计算机内部信息表示的基础,还广泛应用于计算机科学的各个领域。
4.1 数据存储
计算机中的所有数据,包括文本、图像、音频、视频等,最终都以二进制的形式存储在内存或硬盘中。二进制数的简洁性使得数据存储和传输变得高效。
4.2 逻辑运算
计算机内部的逻辑运算(如与、或、非、异或等)都是基于二进制数的。这些运算构成了计算机程序执行的基础,使得计算机能够处理复杂的任务。
4.3 编码与解码
在数据传输和通信过程中,数据经常需要进行编码和解码。二进制编码(如ASCII码、UTF-8等)是数据交换的通用语言,确保了信息的准确传递。
4.4 加密算法
许多现代加密算法都依赖于二进制的运算特性来实现数据的安全传输和存储。通过对二进制
-
 二进制如何轻松转换为十进制?资讯攻略02-28
二进制如何轻松转换为十进制?资讯攻略02-28 -
 揭秘数字魔法:轻松掌握十进制到二进制的转换秘籍资讯攻略11-04
揭秘数字魔法:轻松掌握十进制到二进制的转换秘籍资讯攻略11-04 -
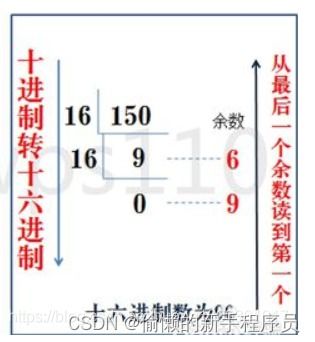 轻松掌握:16进制转10进制的方法资讯攻略02-23
轻松掌握:16进制转10进制的方法资讯攻略02-23 -
 二进制与十进制数的相互转换资讯攻略01-29
二进制与十进制数的相互转换资讯攻略01-29 -
 揭秘二进制到十进制的神奇转换资讯攻略11-09
揭秘二进制到十进制的神奇转换资讯攻略11-09 -
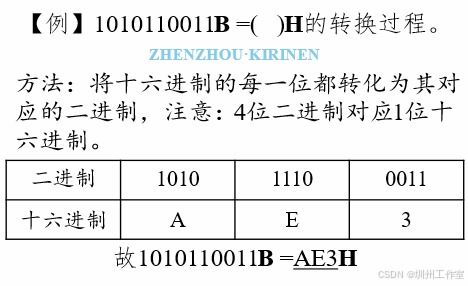 十六进制转换方法指南资讯攻略02-22
十六进制转换方法指南资讯攻略02-22










