揭秘数字魔法:轻松掌握十进制到二进制的转换秘籍
十进制如何转换为二进制
十进制数转换为二进制数,是计算机科学和信息技术中的基础概念。在计算机内部,所有的数据都是以二进制形式存储和处理的。因此,了解十进制与二进制之间的转换方法,对于理解计算机的工作原理至关重要。以下,我们将详细介绍十进制如何转换为二进制,并提供具体的步骤和示例。

首先,我们需要明确什么是十进制和二进制。十进制是我们日常生活中最常用的数制,它基于10个不同的符号(0-9)来表示数值。而二进制则是计算机中使用的数制,它只包含两个符号:0和1。在二进制系统中,每一位(bit)只能是0或1,这使得二进制数在逻辑运算和存储方面非常高效。
接下来,我们介绍十进制转换为二进制的步骤:
1. 除以2取余数法
这是最常用的十进制转二进制的方法。具体步骤如下:
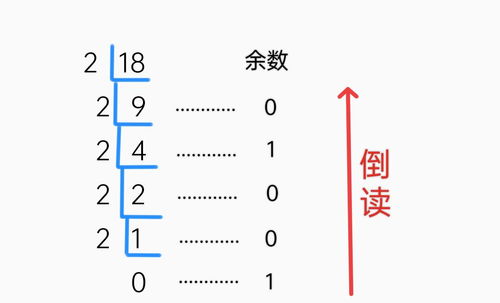
首先,将十进制数除以2,得到商和余数(余数只能为0或1)。
然后,将商再次除以2,又得到新的商和余数。
重复上述步骤,直到商为0为止。
最后,将每一步得到的余数从最后一步开始,依次向前排列,即可得到该十进制数的二进制表示。
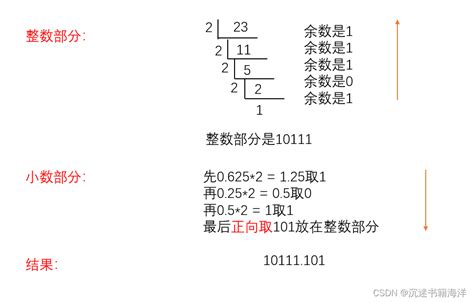
示例:将十进制数23转换为二进制。
23 ÷ 2 = 11 余 1
11 ÷ 2 = 5 余 1
5 ÷ 2 = 2 余 1
2 ÷ 2 = 1 余 0
1 ÷ 2 = 0 余 1
将余数从最后一步开始依次排列,得到23的二进制表示为10111。
2. 不断乘以2取整数部分法
这种方法从十进制数的小数点后开始处理,主要用于处理包含小数部分的十进制数。但为简化说明,我们先以整数部分为例。
首先,将十进制数视为小数(即在其后加一个小数点和一个0)。
然后,不断将该小数乘以2,并记录下每次乘积的整数部分。
重复上述步骤,直到乘积的小数部分变为0(对于有限的十进制小数,这是可能的;对于无限循环小数,则需要截取有限位)。
最后,将每一步得到的整数部分从第一步开始依次排列,即可得到该十进制数的二进制表示(注意:对于整数部分,这种方法的结果与“除以2取余数法”相同,但步骤顺序相反)。
然而,对于整数而言,这种方法相对繁琐且不如“除以2取余数法”直观。因此,在实际应用中,我们更多地使用“除以2取余数法”。不过,在处理包含小数部分的十进制数时,“不断乘以2取整数部分法”就显得尤为重要了。
示例(仅考虑整数部分,以23为例):
23(视为23.0),乘以2得46.0,整数部分为46(但这里我们只需记录每一位新增的整数,即首次的0,然后是6,但实际操作中直接从23.0开始看变化即可,因为整数部分始终未变,这里是为了说明方法而展开)。实际上,这里应直接记录每一步小数乘以2后是否进位到整数位及该位的值(对于23这个整数,始终为0进位然后记录为无变化,直到开始处理小数部分)。但为简化说明,我们假设从23.0开始,并关注其后的变化(尽管整数部分始终为23的等价表示,即始终未变,我们关注的是小数点的移动和新增的整数位):
若考虑将23视为23.000...(无限个0),则首次乘以2后变为46.000...,整数部分未变(仍为23的等价,即46的前两位,但这里我们只关注新增的整数“表示位”,即原本的小数点后的第一位是否进位到整数,对于23这样的整数,始终为0进位),我们关注的是小数点后的变化。但为符合此方法说明,我们假设记录每一步的“整数增加部分”(对于整数而言,即每次乘以2后是否有多余的1进位到原本的小数点前的整数位,但23这样的整数始终为0进位,所以我们直接跳到小数部分的说明,因为整数部分用此方法说明较为繁琐且不直观)。
(注意:上述说明是为了解释方法而展开,实际上对于整数,我们直接使用“除以2取余数法”更为简便。这里的说明是为了展示“不断乘以2取整数部分法”在处理包含小数部分的十进制数时的应用,并指出其在处理整数时的繁琐性。)
对于小数部分的处理(此例中23为整数,所以此
- 上一篇: 中国地板十大知名品牌揭秘
- 下一篇: 快手直播开通全攻略:轻松解锁直播新世界!
-
 揭秘二进制到十进制的神奇转换资讯攻略11-09
揭秘二进制到十进制的神奇转换资讯攻略11-09 -
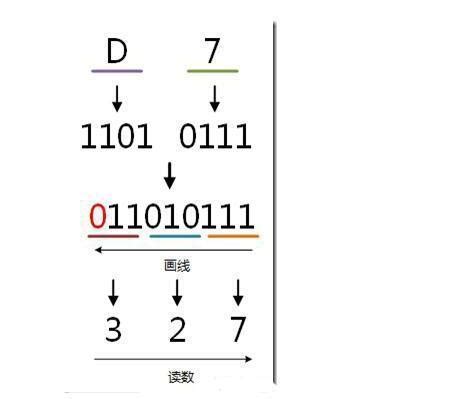 如何将二进制轻松转换为八进制?资讯攻略10-28
如何将二进制轻松转换为八进制?资讯攻略10-28 -
 二进制轻松转换为十进制的方法资讯攻略11-09
二进制轻松转换为十进制的方法资讯攻略11-09 -
 解码数字奥秘:二进制与十进制互转全攻略,轻松掌握转换技巧!资讯攻略10-24
解码数字奥秘:二进制与十进制互转全攻略,轻松掌握转换技巧!资讯攻略10-24 -
 二进制转十进制与十进制转二进制,轻松掌握转换技巧!资讯攻略10-24
二进制转十进制与十进制转二进制,轻松掌握转换技巧!资讯攻略10-24 -
 二进制怎么转换成十进制?资讯攻略11-09
二进制怎么转换成十进制?资讯攻略11-09












