探索数学奥秘:ln1、ln(-1)、Ln1、Ln(-1)的神奇值是多少?
在数学的世界里,对数和复数是两个引人入胜且相互交织的主题。当我们探讨ln1、ln(-1)、Ln1以及Ln(-1)这四个表达式时,实际上是在探究自然对数(以e为底的对数)和复数对数函数的性质。让我们逐一分析这些表达式的含义和结果。

首先,我们来看ln1。在数学中,自然对数ln(x)定义为以e(约等于2.71828)为底的对数,即求解方程e^y = x中的y值。当x=1时,方程变为e^y = 1。我们知道,e的任何0次幂都等于1,即e^0 = 1。因此,y=0是方程e^y = 1的唯一解。所以,ln1 = 0。这个结论表明,1的自然对数值是0,这是一个直观且容易理解的数学事实。

接下来,我们分析ln(-1)。在自然数和对数函数的常规定义下,ln(-1)是一个没有实数值的表达式。因为自然对数的定义域是正实数,不包括负数或零。当尝试求解ln(-1)时,我们试图找到一个实数y,使得e^y = -1。然而,e的任何实数次幂都是正数,因此不存在这样的实数y。所以,在实数范围内,ln(-1)是无定义的。但是,如果我们扩展数系到复数,就可以找到一个解。在复数平面上,-1可以表示为i^2(其中i是虚数单位,满足i^2 = -1)。因此,ln(-1) = ln(i^2) = 2ln(i)。进一步求解ln(i),我们得到ln(i) = πi/2(通过欧拉公式e^(πi) = -1推导得出)。所以,ln(-1) = 2(πi/2) = πi。这个结论表明,在复数范围内,ln(-1)有一个特定的值,即πi。
现在,我们转向Ln1和Ln(-1)的分析。在这里,大写的Ln通常用来表示复数对数函数,它是一个多值函数,能够处理复数输入并返回复数输出。复数对数函数Ln(z)可以表示为ln|z| + iArg(z),其中|z|是z的模(即z的绝对值),Arg(z)是z的辐角(即z在复数平面上与正实轴之间的夹角)。对于Ln1,我们仍然有|1| = 1和Arg(1) = 0(因为1位于复数平面的正实轴上)。所以,Ln1 = ln1 + i0 = 0。这与自然对数ln1的结果相同,因为对于正实数,复数对数函数和自然对数函数在实数范围内是一致的。
最后,我们来看Ln(-1)。对于-1,模仍然为1,但辐角为π(因为-1位于复数平面的负实轴上,与正实轴之间的夹角为π)。所以,Ln(-1) = ln1 + iπ = iπ。这个结论与自然对数在复数范围内的结果ln(-1) = πi一致。然而,值得注意的是,复数对数函数Ln(z)是一个多值函数,因为它依赖于辐角的选择。辐角Arg(z)在复数平面上不是唯一的,因为可以通过添加2π的整数倍来改变辐角而不改变z的值。因此,Ln(-1)实际上是一个无限多个值的集合,可以表示为{iπ + 2πki | k ∈ Z},其中Z表示整数集。这意味着Ln(-1)不仅有iπ这一个值,还有iπ + 2πki(k为任意整数)这些值。然而,在常规的数学讨论中,我们通常只关注主值(即k=0时的值),即iπ。
综上所述,我们对ln1、ln(-1)、Ln1以及Ln(-1)这四个表达式进行了详细的分析。ln1和Ln1都等于0,这是因为在实数范围内(对于自然对数)和复数范围内(对于复数对数函数),1的对数值都是0。ln(-1)在实数范围内是无定义的,但在复数范围内等于πi,这是通过欧拉公式推导得出的。同样地,Ln(-1)也是一个多值函数,其主值为iπ,但它实际上包含了一个无限多个值的集合。这些结论不仅揭示了自然对数和复数对数函数的性质,还展示了复数在数学中的独特魅力和广泛应用。
在数学的学习和研究中,我们经常会遇到看似简单却深藏奥秘的表达式。通过对这些表达式的深入分析和探讨,我们能够更好地理解数学的本质和魅力。同时,这些结论也在科学、工程、物理学等领域中发挥着重要的作用。因此,我们应该保持对数学的好奇心和探索精神,不断挖掘数学中的宝藏和奥秘。
- 上一篇: 轻松学会包花技巧,打造精美花束
- 下一篇: 如何轻松绘制网络图?
-
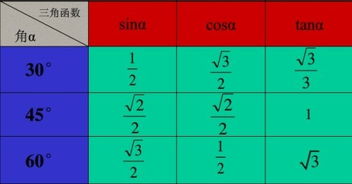 30度角的余弦值是多少资讯攻略10-30
30度角的余弦值是多少资讯攻略10-30 -
 揭秘复数的神奇世界:探索数学中的另一个维度资讯攻略11-16
揭秘复数的神奇世界:探索数学中的另一个维度资讯攻略11-16 -
 揭秘!直角三角形面积计算的神奇公式,一学就会的几何奥秘资讯攻略10-24
揭秘!直角三角形面积计算的神奇公式,一学就会的几何奥秘资讯攻略10-24 -
 鹰嘴豆的具体热量值是多少资讯攻略11-06
鹰嘴豆的具体热量值是多少资讯攻略11-06 -
 探索黄金比例的奥秘:如何精准计算这一美学奇迹?资讯攻略02-04
探索黄金比例的奥秘:如何精准计算这一美学奇迹?资讯攻略02-04 -
 揭秘数学奥秘:合数、约数、质数与素数的深度解析资讯攻略11-27
揭秘数学奥秘:合数、约数、质数与素数的深度解析资讯攻略11-27











