揭秘数学奥秘：合数、约数、质数与素数的深度解析

在数学领域中，理解数的性质是探索数学奥秘的重要一环。其中，合数、约数、质数（素数）这几个概念，构成了理解整数性质的基础框架。本文旨在清晰、简洁地介绍这些概念，帮助读者建立扎实的数学基础，同时注重内容的结构性和搜索引擎友好度，确保信息的有效传达。

首先，我们从“约数”这一基本概念入手。约数，简单来说，就是一个数能被整除的数。如果一个整数a可以被另一个整数b整除（b≠0），那么我们就说b是a的一个约数。例如，12的约数有1、2、3、4、6和12本身。值得注意的是，每个数的约数都包括1和它本身，这是约数定义的两个基本元素。此外，一个数的约数还可以是其他小于它且能整除它的正整数。约数的概念是理解其他数论概念的基础，它揭示了数之间的一种整除关系。

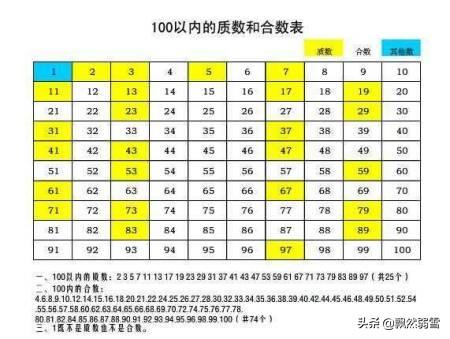
接下来，我们探讨“质数”（素数）的概念。质数是一个大于1的自然数，除了1和它本身以外不再有其他约数。换句话说，质数只能被1和自己整除。例如，2、3、5、7等都是质数，它们不能分解为两个大于1的整数之积。质数是数论中的基本构建块，许多数学问题都围绕质数展开。质数的定义简洁而深刻，它反映了数的纯粹性——一个数如果只能被1和自己整除，那么这个数就是质数。值得注意的是，1不是质数，因为它只有一个约数（即自身），不符合质数的定义中“除了1和它本身以外不再有其他约数”的条件。

与质数相对的是“合数”。合数是一个大于1的自然数，并且除了1和它本身以外还有其他约数。换句话说，合数可以分解为两个或两个以上大于1的整数之积。例如，4、6、8、9等都是合数，因为它们除了1和自己以外还有其他约数。合数与质数构成了自然数中除1以外的两大类，它们共同构成了自然数的完整图景。合数的存在体现了数的复杂性，一个数如果能被多个数整除，那么这个数就是合数。

质数和合数的概念在数论中占据着举足轻重的地位。它们不仅是数学研究的基本对象，还是密码学、计算机科学等领域的重要工具。例如，在密码学中，质数的性质被用来构建安全的加密算法；在计算机科学中，质数和合数的判断是算法设计的基础问题之一。此外，质数和合数的概念还与数学中的其他领域紧密相连，如素数定理、哥德巴赫猜想等著名数学问题都涉及质数的性质。

在深入探讨这些概念时，我们还会发现一些有趣的数学现象。例如，所有大于2的偶数都是合数，因为它们都可以被2整除。这一性质使得偶数与质数之间形成了一种天然的“隔阂”——除了2以外，质数都是奇数。这一现象揭示了数与数之间隐藏的规律，也激发了数学家们对质数分布规律的深入研究。

此外，关于质数和合数，还有一个著名的猜想——哥德巴赫猜想。该猜想提出，任何一个大于2的偶数都可以表示为两个质数之和。例如，4=2+2（虽然2是唯一的偶数质数，但在此特殊情况下仍满足条件），6=3+3，8=3+5，等等。尽管这个猜想已经被数学家们验证了无数个特例，但至今仍未得到一般性的证明。哥德巴赫猜想是数论中的一个未解之谜，它挑战着数学家们的智慧和耐心。

除了哥德巴赫猜想外，质数和合数还与许多其他数学问题紧密相连。例如，素数定理指出，在任意大的正整数n附近，约有一半的数是质数。这一定理揭示了质数在自然数中的分布规律，是数论研究中的重要成果之一。此外，费马小定理、欧拉定理等著名定理也涉及质数的性质，它们在数论、代数等领域有着广泛的应用。

在结束这篇文章之前，我们再简要回顾一下这些概念之间的联系和区别。约数是数之间整除关系的体现，它揭示了数的一种基本性质。质数（素数）和合数则是根据数的约数数量来划分的两类数。质数只有1和自己两个约数，体现了数的纯粹性；而合数则有多个约数，体现了数的复杂性。这三者共同构成了自然数的完整图景，为我们探索数学世界提供了丰富的素材和工具。

总之，合数、约数、质数（素数）这些概念是数学中不可或缺的基本元素。它们不仅揭示了数的内在性质，还为数学研究提供了有力的工具和方法。通过深入理解和应用这些概念，我们可以更好地探索数学世界的奥秘，发现数学之美。同时，这些概念也是数学与其他学科交叉融合的桥梁，它们在科学、工程、技术等领域发挥着重要作用。因此，对于任何一个热爱数学的人来说，掌握这些基本概念都是至关重要的。