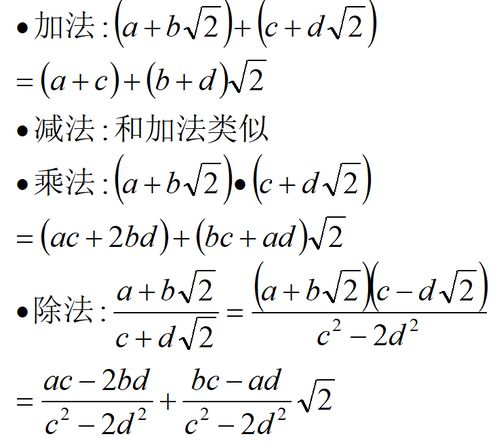什么是有理数?能举些常见的有理数例子吗?
当我们深入探讨数学的广阔领域时,不可避免地会遇到一个基础而重要的概念——有理数。这个词汇,虽然听起来略显抽象,实则在我们的日常生活中有着广泛的应用与体现。那么,究竟什么是有理数呢?哪些数可以被归类为有理数呢?接下来,就让我们一起揭开有理数的神秘面纱。

有理数的定义
首先,让我们从定义入手。有理数,顾名思义,是“可以表示为两个整数之比的数”,这里的“整数”包括正整数、零和负整数。具体地说,一个数如果可以被写成a/b(a和b是整数,且b不等于0)的形式,那么这个数就是有理数。这个定义揭示了有理数的本质特征,即它们都是可以通过整数运算(加、减、乘、除,但除数不能为0)得到的数。

有理数的分类
有理数可以根据其正负性和小数表现形式进行分类。
1. 正有理数:所有大于0的有理数,如1/2、3/4、7等,它们在小数表示中可以是有限小数(如0.5、0.75)或无限循环小数(如1/3=0.333...)。
2. 零:虽然零是整数的一个特例,但它同样满足有理数的定义(0/1或任何非零整数之比),因此也被视为有理数的一员。
3. 负有理数:所有小于0的有理数,如-1/2、-3/4等,它们的小数表示同样可以是有限小数(如-0.5)或无限循环小数(如-1/3=-0.333...)。
有理数的例子
为了更好地理解有理数,我们可以列举一些具体的例子:
整数都是有理数:因为任何整数都可以表示为它本身与1的比值,比如5=5/1,-3=-3/1。
分数:自然是有理数的典型代表,如1/4、2/3、5/6等,它们都符合两个整数之比的定义。
有限小数:所有有限小数都可以转化为分数形式,因此它们也是有理数。例如,0.25=1/4,0.666...=2/3(虽然这个例子看起来像是循环小数,但实际上是有限小数的近似表示)。
循环小数:如前面提到的1/3=0.333...、2/7=0.285714285714...等,这些数在小数点后有规律地重复某些数字,它们都可以转化为分数形式,因此也是有理数。
有理数的性质
有理数集合在数学上具有丰富的性质,以下是一些基本的性质:
封闭性:在有理数集中,进行加、减、乘、除(除数不为0)运算后,结果仍然是有理数。
稠密性:在任意两个不相等的有理数之间,总可以找到无数个有理数。
有序性:有理数集可以按照大小进行排序,满足传递性、反对称性和完全性。
可数性:有理数集是可数的,即可以一一列举出来,尽管其数量在直觉上似乎无穷无尽。
有理数与无理数的区别
在探讨有理数的同时,我们不得不提到与之对应的另一类数——无理数。无理数是不能表示为两个整数之比的数,它们的小数表示是无限不循环的,如π(圆周率)、e(自然对数的底数)以及根号下不能开方为整数的数(如√2)。无理数与有理数在数轴上共同构成了实数集,但它们在性质和表现形式上有着本质的区别。
结语
综上所述,有理数作为数学中的一个基本概念,不仅承载着深厚的理论意义,还与我们的日常生活紧密相连。从简单的分数计算到复杂的数学问题,有理数都扮演着举足轻重的角色。通过了解其定义、分类、例子及性质,我们可以更加深刻地认识到有理数在数学王国中的重要地位,也为进一步探索数学的奥秘奠定了坚实的基础。
- 上一篇: 一键直达!手机人人通学生专属登录入口
- 下一篇: 小米手机:如何设置应用通过手机号一键登录权限
-
 全面解析实数:定义与生动实例资讯攻略11-21
全面解析实数:定义与生动实例资讯攻略11-21 -
 如何定义和理解有理数是什么?资讯攻略11-04
如何定义和理解有理数是什么?资讯攻略11-04 -
 深度解析:什么是有理数?一文带你全面了解资讯攻略10-26
深度解析:什么是有理数?一文带你全面了解资讯攻略10-26 -
 有理化秘籍:轻松掌握化简技巧资讯攻略10-31
有理化秘籍:轻松掌握化简技巧资讯攻略10-31 -
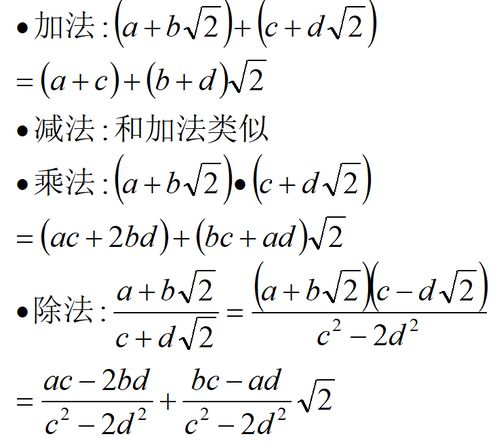 揭秘无理数的神秘面纱资讯攻略11-05
揭秘无理数的神秘面纱资讯攻略11-05 -
 数轴上有理数abc的位置解析资讯攻略03-18
数轴上有理数abc的位置解析资讯攻略03-18