揭秘无理数的神秘面纱

在数学的世界里，有一类数字既神秘又引人深思，它们无法表示为两个整数的比，即不能写成a/b（a、b为整数，b≠0）的形式，这类数字被统称为无理数。无理数的概念最早可以追溯到古希腊时期，数学家们在对几何量进行度量时，发现某些长度或面积无法用有理数精确表示，从而开启了无理数研究的先河。

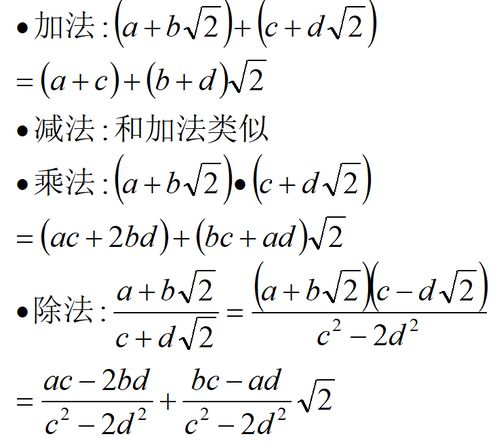
无理数的定义与特性

无理数，顾名思义，就是“没有理由”（无法用有理数形式表示）的数。它们在小数展开后既不终止也不循环，这一特性使得无理数在数值处理上显得尤为特殊。例如，常见的无理数π（圆周率）和√2（2的平方根），它们的小数点后既不会结束，也不会重复出现相同的数字序列。

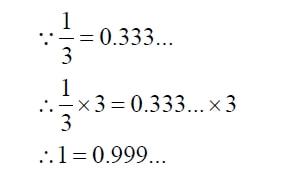
无理数的发现历程

无理数的发现，是数学史上的一次重大革命。古希腊数学家毕达哥拉斯学派曾坚信“万物皆数”，这里的“数”指的是有理数。然而，当毕达哥拉斯的学生希帕索斯发现正方形的对角线与其边长之比无法用有理数表示时，这一信念受到了严重挑战。这一发现，即√2是无理数，不仅打破了当时数学界的认知框架，还引发了关于数学本质的深刻讨论，甚至导致了希帕索斯被学派视为异端而遭受不幸。

无理数与有理数的区别

为了更清晰地理解无理数，我们需要将其与有理数进行对比。有理数，顾名思义，就是“有道理”的数，它们可以表示为两个整数的比。有理数包括整数、分数和有限小数或无限循环小数。相比之下，无理数则无法以这种形式表示，它们的小数展开是无限不循环的。这种差异，使得无理数在数轴上的分布更加稠密，几乎占据了数轴上的每一个点，而有理数则只能占据可数无穷多个点。

无理数的应用实例

无理数在现实生活中的应用广泛而深远。以π为例，它是圆的周长与直径之比，是数学、物理、工程等多个领域不可或缺的基本常数。从计算圆的面积、周长，到分析波动现象、量子力学中的概率分布，π的身影无处不在。另一个重要的无理数e（自然对数的底数），在复利计算、人口增长模型、放射性衰变等自然现象的描述中发挥着关键作用。此外，黄金分割比φ（约等于1.618），作为自然界中最美的比例之一，在建筑、艺术、生物学等领域都有着广泛的应用。

无理数的证明方法

证明一个数是无理数，通常需要运用反证法。以√2为例，假设√2是有理数，那么它可以表示为两个互质的整数p和q的比（p/q），且p和q没有公因数（除了1）。根据这个假设，我们可以推导出2q²=p²，这意味着p必须是偶数。设p=2r（r为整数），代入上式得到4r²=2q²，化简得q²=2r²，同样说明q也是偶数。这与p和q互质的假设相矛盾，因此假设不成立，√2是无理数。

无理数的十进制表示与近似计算

无理数在十进制下的表示是无限不循环小数，这意味着我们无法精确写出其完整数值。然而，在实际应用中，我们往往只需要无理数的近似值。例如，π的近似值有3.14、3.14159等，根据需要的精度选择合适的近似值。对于无理数的近似计算，有多种方法，如级数展开（如泰勒级数）、连分数表示、蒙特卡洛模拟等。

无理数与数学基础

无理数的引入，不仅丰富了数学的内容，还促进了数学基础理论的深化。在实数系的构建中，无理数与有理数共同构成了完整的实数集。实数系的连续性、完备性等性质，在很大程度上依赖于无理数的存在。此外，无理数在微积分、复变函数、数论等数学分支中扮演着重要角色，是连接不同数学领域的桥梁。

无理数与计算机科学

随着计算机科学的兴起，无理数的研究和应用也进入了新的阶段。在计算机内部，无理数通常以浮点数或符号计算软件中的精确表示形式存储和处理。浮点数的精度受限于其表示方式（如IEEE 754标准），这可能导致在计算过程中出现舍入误差。而符号计算软件则能够处理高精度的无理数运算，为科学研究提供了强有力的工具。

无理数与哲学思考

无理数的发现，不仅在数学领域引起了轰动，还激发了哲学家对数学本质、无穷大、连续性等概念的深入思考。康德、黑格尔等哲学家，都曾对无理数及其背后的数学逻辑进行过探讨，认为它们揭示了自然界和人类思维中的某种深刻规律。无理数的存在，让我们意识到数学不仅仅是计算的工具，更是探索宇宙奥秘、理解人类认知的重要途径。

结语