掌握图形旋转的三大必备技巧

在图形处理和计算机图形学中，旋转是一种基本且重要的变换操作。通过旋转，我们可以改变图形的方向，从而创造出丰富的视觉效果。本文将详细介绍图形旋转的三种主要方法：手动计算旋转矩阵、使用图形库函数以及基于坐标变换的旋转。无论你是图形设计师、编程爱好者还是计算机图形学的学生，掌握这些方法都将对你的工作和学习大有裨益。

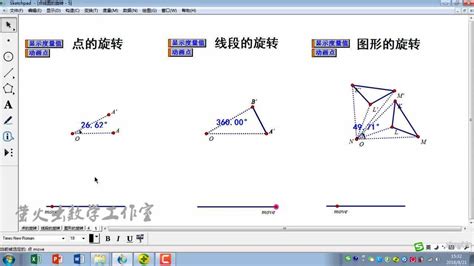
一、手动计算旋转矩阵

手动计算旋转矩阵是实现图形旋转最直接的方法。这种方法的核心在于理解二维平面上的旋转公式，并据此构建旋转矩阵。旋转矩阵能够将原始图形的每个顶点映射到旋转后的新位置。

1.1 二维旋转公式

在二维平面上，一个点 (x, y) 绕原点旋转角度 θ 后的新坐标 (x', y') 可以通过以下公式计算：

\[

x' = x \cos(\theta) - y \sin(\theta)

\]

\[

y' = x \sin(\theta) + y \cos(\theta)

\]

这里的 cos(θ) 和 sin(θ) 分别是角度 θ 的余弦值和正弦值。

1.2 旋转矩阵

上述公式可以写成矩阵形式：

\[

\begin{bmatrix}

x' \\

y'

\end{bmatrix}

\begin{bmatrix}

\cos(\theta) & -\sin(\theta) \\

\sin(\theta) & \cos(\theta)

\end{bmatrix}

\begin{bmatrix}

x \\

\end{bmatrix}

\]

这个 2x2 的矩阵就是旋转矩阵。通过矩阵乘法，我们可以将原始图形的所有顶点转换为旋转后的新坐标。

1.3 示例

假设我们有一个点 (1, 0)，想要将其绕原点旋转 90 度。根据旋转矩阵，我们可以计算：

\[

\begin{bmatrix}

x' \\

y'

\end{bmatrix}

\begin{bmatrix}

\cos(90^\circ) & -\sin(90^\circ) \\

\sin(90^\circ) & \cos(90^\circ)

\end{bmatrix}

\begin{bmatrix}

1 \\

\end{bmatrix}

\begin{bmatrix}

0 & -1 \\

1 & 0

\end{bmatrix}

\begin{bmatrix}

1 \\

\end{bmatrix}

\begin{bmatrix}

0 \\

\end{bmatrix}

\]

因此，点 (1, 0) 旋转 90 度后变为 (0, 1)。

二、使用图形库函数

虽然手动计算旋转矩阵是理解图形旋转原理的好方法，但在实际应用中，我们通常会使用图形库提供的旋转函数来简化操作。这些函数封装了旋转矩阵的计算过程，使得旋转操作更加便捷和高效。

2.1 图形库简介

不同的编程语言和图形平台提供了不同的图形库。例如，在 HTML5 Canvas 中，我们可以使用 `rotate` 方法；在 OpenGL 中，有 `glRotatef` 函数；在 Python 的 PIL（Pillow）库中，有 `rotate` 方法；而在 Matplotlib 中，则可以通过设置变换矩阵来实现旋转。

2.2 HTML5 Canvas 示例

在 HTML5 Canvas 中，我们可以使用 `ctx.rotate(angle)` 方法来旋转画布。需要注意的是，这里的旋转是相对于当前的原点进行的，因此通常需要先移动画布的原点到图形的中心，然后再进行旋转。

```html

var canvas = document.getElementById('myCanvas');

var ctx = canvas.getContext('2d');

// 绘制一个矩形作为示例

ctx.fillRect(50, 50, 100, 100);

// 移动画布的原点到矩形的中心

ctx.translate(100, 100);

// 旋转画布 45 度

ctx.rotate(45 * Math.PI / 180);

// 再次绘制矩形，此时它会绕中心旋转 45 度

ctx.fillRect(-50, -50, 100, 100);

```

2.3 OpenGL 示例

在 OpenGL 中，我们可以使用 `glRotatef(angle, x, y, z)` 函数来旋转当前矩阵。这里的 `x, y, z` 表示旋转轴的方向，而 `angle` 是旋转角度