揭秘长方体周长:轻松掌握计算公式
长方体,作为一种在日常生活中极为常见的三维几何形状,无论是建筑物的墙体、家具的构造,还是我们手中握持的包装盒,都广泛存在着它的身影。对于许多人来说,了解长方体的基本属性,特别是如何计算其周长(或者说表面积中的边缘总长),是一项既实用又充满趣味的知识。尽管传统意义上,“周长”一词更多地与二维图形相关,但在三维空间中,通过分解长方体,我们同样可以探讨其边缘的总长度。本文将深入浅出地介绍长方体的周长计算方法,让感兴趣的你轻松掌握这一技能。
首先,我们需要明确一点:长方体并没有一个直接的“周长”概念,因为周长通常指的是二维平面图形边缘的总长度。然而,在三维空间中,如果我们想要得到长方体所有边的总长度,可以将其视为由六个矩形面组成,每个面都有其周长。因此,长方体的“总边缘长度”可以通过计算所有矩形面的周长之和(但需去除重复计算的边)来近似得到。为简化讨论,本文中提到的“长方体的周长”实际上是指其所有十二条边的总长度。
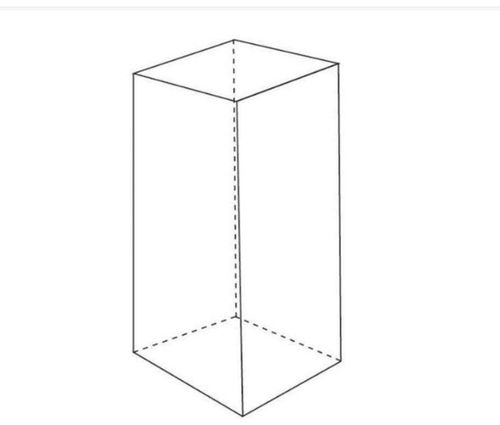
长方体的基本结构
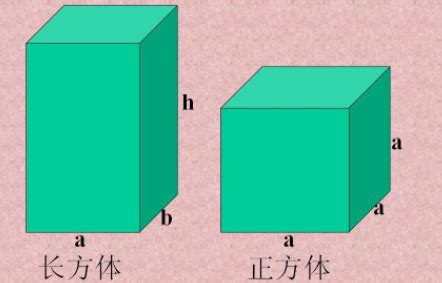
长方体的结构非常简单明了:它由六个矩形面组成,其中每对面都是平行的,并且大小相等。具体来说,长方体有三组平行的边,每组包含四条等长的边。我们通常用长(L)、宽(W)、高(H)来描述一个长方体的尺寸。

计算长方体各边的总长度
由于长方体有三组平行的边,每组四条,因此总共有12条边。每组边的长度分别是长(L)、宽(W)和高(H)。为了计算所有边的总长度,我们只需将每种长度的边数乘以对应的边长,然后将结果相加。
1. 长边:长方体有4条长度为L的边。
2. 宽边:长方体有4条长度为W的边。
3. 高边:长方体有4条长度为H的边。
因此,长方体所有边的总长度为:
总长度 = 4L + 4W + 4H
这个公式简单明了,只需要知道长方体的长、宽、高三个尺寸,就能快速计算出其所有边的总长度。
长方体“周长”的应用场景
虽然长方体没有严格的“周长”定义,但计算其所有边的总长度在实际应用中具有重要意义。例如:
材料估算:在制作需要精确尺寸的长方体物品时,了解所有边的总长度有助于准确估算所需材料的量,从而避免浪费或不足。
包装设计:在设计包装时,计算长方体的总边缘长度可以帮助设计师确定包装材料的尺寸和用量,确保产品能够安全、美观地包装起来。
建筑计算:在建筑设计中,计算长方体(如墙体)的边缘总长度对于估算建筑材料的消耗、规划施工步骤等至关重要。
长方体与其他几何体的比较
将长方体的“周长”计算方法与其他几何体进行比较,有助于我们更全面地理解这一概念。
球体:球体没有直线边缘,因此没有“周长”的概念,但可以通过计算其表面积来间接了解。
圆柱体:圆柱体有两个平行的圆形底面和一个侧面。虽然底面的周长(即圆的周长)可以计算,但整个圆柱体的“周长”则比较复杂,通常通过计算其表面积来反映。
正方体:正方体是长方体的特例,其中长、宽、高都相等。计算其所有边的总长度同样遵循上述公式,只是L=W=H。
长方体周长计算的注意事项
在计算长方体所有边的总长度时,有几个关键点需要注意:
准确性:确保输入的长、宽、高尺寸准确无误,这是计算正确性的基础。
单位统一:如果尺寸使用不同的单位(如厘米和米),需要先进行单位转换,以保证计算结果的准确性。
实际应用:虽然本文讨论的是长方体的“周长”,但在实际应用中,可能需要根据具体情况进行适当调整,如考虑边缘的磨损、材料的弹性等因素。
长方体周长的实际应用案例
为了更好地理解长方体周长的计算方法及其实际应用,让我们来看一个具体的例子。
假设我们要为一个尺寸为50厘米×30厘米×20厘米的长方体物品制作一个保护套。为了确定保护套所需材料的量,我们需要计算长方体所有边的总长度。
长(L)= 50厘米
宽(W)= 30厘米
高(H)= 20厘米
根据公式:总长度 = 4L + 4W + 4H
代入数值:总长度 = 4×50 + 4×30 + 4×20 = 200 + 120 + 80 = 400厘米
因此,制作这个保护套需要大约400厘米的材料(不考虑裁剪、拼接等过程中的损耗)。这个计算结果为我们的材料采购和制作提供了重要的参考依据。
结语
通过本文的介绍,我们了解了长方体“周长”的计算方法及其实际应用。虽然长方体没有严格的“周长”定义,但通过计算其所有边的总长度,我们可以获得一个有用的数值,用于指导材料估算、包装设计和建筑计算等多个领域。掌握这一技能不仅能够帮助我们更好地理解和应用几何知识,还能在实际生活中发挥重要作用。希望本文的内容能够激发你对长方体及其相关计算的兴趣,让你在探索几何世界的道路上越走越远。
- 上一篇: 如何计算9寸披萨的面积?
- 下一篇: 武大郎炊饼今何在?揭秘其与现代哪种美食最相似
-
 揭秘长方体周长计算的奥秘公式资讯攻略11-14
揭秘长方体周长计算的奥秘公式资讯攻略11-14 -
 长方体周长怎么计算?资讯攻略11-13
长方体周长怎么计算?资讯攻略11-13 -
 正方形周长的计算公式是什么资讯攻略11-01
正方形周长的计算公式是什么资讯攻略11-01 -
 三角形周长计算:使用周长公式的方法资讯攻略11-11
三角形周长计算:使用周长公式的方法资讯攻略11-11 -
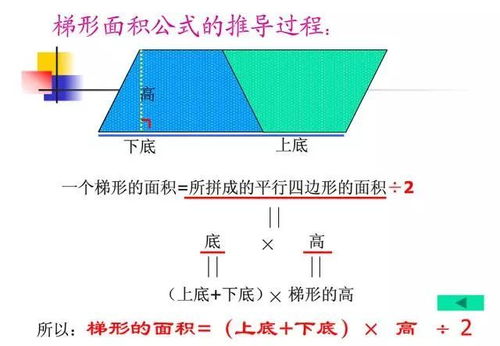 平行四边形与梯形的面积及周长计算公式资讯攻略12-06
平行四边形与梯形的面积及周长计算公式资讯攻略12-06 -
 揭秘长方体表面积的神奇计算公式!资讯攻略12-07
揭秘长方体表面积的神奇计算公式!资讯攻略12-07












