平行四边形与梯形的面积及周长计算公式

在几何学中，平行四边形和梯形是两种常见的四边形，它们在日常生活中无处不在，从建筑设计到图形艺术，再到地理测绘，都扮演着重要的角色。掌握它们的面积和周长计算公式，不仅能帮助我们解决实际问题，还能深化对几何图形的理解。本文将详细介绍平行四边形和梯形的面积及周长公式，并通过实例展示如何应用这些公式。

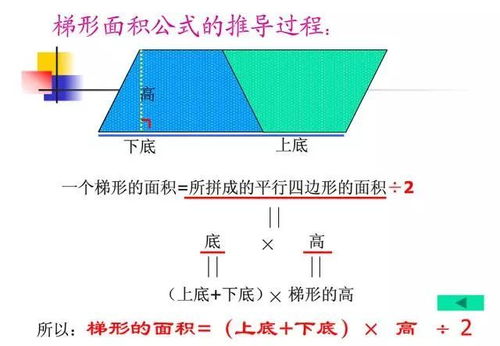
首先，我们来看平行四边形。平行四边形是一种两组对边分别平行且相等的四边形。它的面积计算公式是：面积等于底边长度乘以高。这里的“底边”可以是平行四边形的任意一条边，而“高”则是从这条底边出发，垂直于底边并且连接平行四边形对角顶点的线段。需要注意的是，无论底边和高如何选择，只要保证它们是垂直关系，计算出的面积都是相同的。这是因为平行四边形的对角线将其分为两个等面积的三角形，而三角形的面积计算公式正是底边乘以高的一半，两个这样的三角形加起来就回到了平行四边形的面积公式。

平行四边形的周长计算公式则更为直观：周长等于四条边的长度之和。由于平行四边形的对边相等，因此在实际计算时，只需将两组对边的长度分别相加，再乘以2即可。例如，一个平行四边形的一组对边长度分别为a和b，那么它的周长就是2(a+b)。

接下来，我们讨论梯形。梯形是一种只有一组对边平行的四边形。这组平行的边被称为梯形的上底和下底，而不平行的两边则被称为梯形的腰。计算梯形的面积时，我们使用的是这样的公式：面积等于（上底加下底）乘以高再除以2。这个公式实际上是基于三角形面积公式的推广。如果将梯形的上底和下底看作是两个三角形的底边，而梯形的高则是这两个三角形的高，那么梯形的面积就等于这两个三角形面积的和。由于三角形的面积等于底边乘以高的一半，所以梯形的面积就是（上底加下底）乘以高的一半，即上述公式。

至于梯形的周长计算公式，与平行四边形类似，也是四条边长度之和。不过，由于梯形的两组对边并不相等（只有一组对边平行），所以在计算周长时，需要分别测量并相加每一条边的长度。

为了更好地理解这些公式，我们可以通过一些实例来进行说明。

假设我们有一个平行四边形，它的底边长度为8厘米，高为6厘米。根据平行四边形的面积公式，我们可以计算出它的面积为8厘米乘以6厘米等于48平方厘米。再来看周长，如果它的另外一条与底边平行的边长度为8厘米（因为平行四边形的对边相等），而两条垂直于底边的腰的长度各为5厘米，那么它的周长就是8厘米加8厘米加5厘米加5厘米等于26厘米。

再来看一个梯形的例子。假设我们有一个梯形，它的上底长度为5厘米，下底长度为10厘米，高为7厘米。根据梯形的面积公式，我们可以计算出它的面积为（5厘米加10厘米）乘以7厘米再除以2等于52.5平方厘米。至于周长，如果它的两条腰的长度分别为6厘米和8厘米（这里假设了两条腰的长度不相等，但实际情况中它们可能相等），那么它的周长就是5厘米加10厘米加6厘米加8厘米等于29厘米。

在实际应用中，这些公式可以帮助我们解决许多与面积和周长相关的问题。比如，在建筑设计中，我们可能需要计算一个屋顶的面积来确定需要多少材料来覆盖它；在图形艺术中，我们可能需要根据一个给定周长的平行四边形或梯形来设计一个图案；在地理测绘中，我们可能需要测量一个地块的面积来评估其价值或用途。

此外，这些公式还可以作为我们进一步学习更复杂几何图形的基础。比如，在三维几何中，我们可以将平行四边形看作是一个平面的矩形在三维空间中的投影，从而推导出与之相关的立体图形的面积和体积公式。同样地，梯形也可以作为我们理解更复杂四边形（如不规则四边形）面积计算方法的基础。

最后需要指出的是，虽然这些公式在大多数情况下都是准确的，但在实际应用中我们还是需要注意一些特殊情况。比如，在计算平行四边形的面积时，我们需要确保所选择的高是垂直于底边的；在计算梯形的面积时，我们需要确保所测量的上底和下底是平行的。如果这些条件不满足，那么计算出的面积可能会有误。同样地，在计算周长时，我们也需要确保测量的是图形的所有边而不是部分边或对角线等。

综上所述，平行四边形和梯形的面积和周长公式是几何学中的基础知识之一。掌握这些公式不仅可以帮助我们解决实际问题，还可以为我们进一步学习更复杂的几何图形打下坚实的基础。因此，在学习这些公式时我们应该认真对待每一个细节，确保能够准确理解和应用它们。