二进制转十进制与十进制转二进制，轻松掌握转换技巧！

在数字的世界里，二进制与十进制是两种极为重要且广泛应用的数制。它们分别在不同的领域扮演着关键角色，比如计算机内部数据的存储与处理几乎完全依赖于二进制，而我们在日常生活中则更习惯于使用十进制进行计算与表示。那么，二进制与十进制之间是如何相互转换的呢？下面，我们将直接步入正题，探索这一数字转换的奥秘。

二进制转十进制

二进制，顾名思义，就是基于2的进位制数制。在二进制系统中，仅使用两个数字符号：0和1。二进制转十进制的过程相对直观，主要通过“按权展开”法实现。

方法概述

二进制转十进制的基本思路是将每一位上的数字乘以2的相应次幂（从右往左数，最右边为2的0次幂，然后依次是2的1次幂、2的2次幂……），然后将所有乘积相加，得到的和即为该二进制数对应的十进制数。

实例演示

假设有一个二进制数`1011`，我们按照上述方法进行转换：

最右边的1，对应的是2的0次幂，即`1 * 2^0 = 1`；

接着向左的1，对应的是2的1次幂，即`1 * 2^1 = 2`；

然后是0，对应的是2的2次幂，但由于是0，所以乘积为`0 * 2^2 = 0`；

最左边的1，对应的是2的3次幂，即`1 * 2^3 = 8`。

将这些乘积相加：`1 + 2 + 0 + 8 = 11`。

所以，二进制数`1011`转换为十进制数是`11`。

十进制转二进制

十进制是我们日常生活中最常用的数制，它基于10的进位制。要将十进制数转换为二进制数，则主要采用“除2取余”法。

方法概述

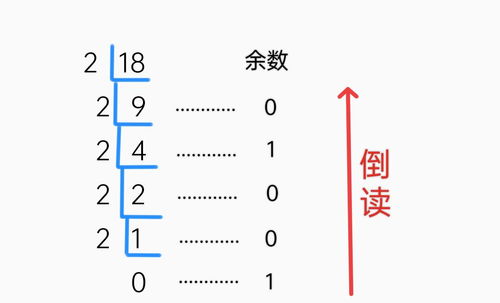
十进制转二进制的过程是通过不断地将十进制数除以2，并记录下每次除法所得的余数，直到商为0为止。然后，将这些余数按相反的顺序排列（即先得到的余数排在后面），所得到的数串即为该十进制数对应的二进制数。

实例演示

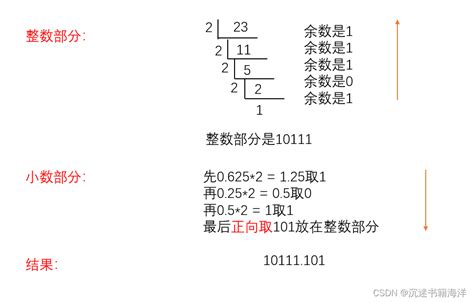
以十进制数`23`为例，我们进行二进制转换：

1. 首先，用23除以2，得到商11余1，记下余数1；

2. 然后，用商11再次除以2，得到商5余1，记下余数1；

3. 接着，用商5除以2，得到商2余1，记下余数1；

4. 最后，用商2除以2，得到商1余0，记下余数0；

5. 继续用商1除以2，得到商0余1，记下余数1，此时商为0，转换过程结束。

将得到的余数按相反的顺序排列：`10111`。

所以，十进制数`23`转换为二进制数是`10111`。

注意事项

在二进制转十进制时，注意每一位的权值（即2的次幂）不要算错。

十进制转二进制时，要持续进行除法操作直至商为0，并确保最后按逆序排列余数。

对于包含小数部分的十进制数转为二进制，整数部分和小数部分的处理方法有所不同，小数部分采用“乘2取整”法，此处不再展开。

通过上述介绍，相信你已经对二进制与十进制之间的转换有了清晰的认识。无论是编程、数据分析，还是日常生活中的一些小技巧，掌握这两种数制之间的转换都是非常有用的。希望这篇文章能够帮助到你，让你在数字的世界里更加游刃有余。