二进制轻松转换为十进制的方法
二进制与十进制,作为计算机科学与日常生活中最为常见的两种数制,它们之间的转换是理解数字世界运作原理的基础。二进制,顾名思义,是以2为基数的数制系统,仅包含0和1两个数字;而十进制,则是以10为基数的数制,由0到9这十个数字组成。在计算机内部,所有信息——无论是文本、图像、音频还是视频——都被转化为二进制代码进行处理和存储。因此,掌握二进制转化为十进制的方法,不仅是学习编程的必经之路,也是深入探索数字技术世界的钥匙。

一、基础原理:从位权到累加
二进制转换为十进制的过程,本质上是一个位权累加的过程。在十进制中,每一位数字所代表的值是其本身乘以10的幂次方,幂次由该位距离小数点的位置决定(从左至右递增,负数表示小数部分)。类似地,在二进制中,每一位数字所代表的值是其本身乘以2的幂次方。这一原则构成了二进制转十进制的基础。

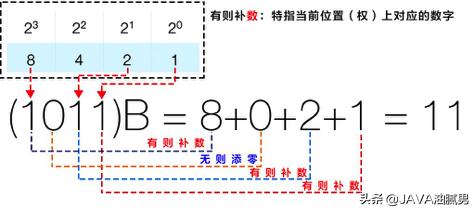
举个例子,二进制数1011转换为十进制数的步骤如下:

从右至左,最右边的位(也称最低位)是2的0次方,即1;

接着往左,是2的1次方,即2;
然后是2的2次方,即4;
最左边的位(也称最高位)是2的3次方,即8。
现在,我们将二进制数1011中每一位的1对应的权值相加:
最右边的1对应1(2^0);
接着的0不贡献值(因为它乘以的是2^1的0,即0);
然后的1对应4(2^2);
最左边的1对应8(2^3)。
因此,二进制数1011转换为十进制的结果是1 + 0 + 4 + 8 = 13。
二、手动计算:实践中的技巧
虽然理解位权是转换的关键,但在实际操作中,通过直接累加每一位的值也能快速完成转换。这种方法特别适合处理位数不多的二进制数。例如,对于二进制数1101:
从右至左,最右边的1代表1(2^0);
接着的0依然不贡献值;
然后的1代表4(2^2,因为跳过了2^1的0);
最左边的1代表8(2^3)。
累加得到:1 + 0 + 4 + 8 = 13,与之前的例子结果一致,但展示了即使遇到连续的0,也能通过跳过它们来简化计算。
三、编程实现:自动化转换
随着数据量的增加,手动转换不仅效率低下,而且容易出错。因此,利用编程语言实现二进制到十进制的自动转换成为必然选择。几乎所有编程语言都提供了内置函数或简单的方法来完成这一任务。
以Python为例,可以通过内置的`int`函数直接实现转换:
```python
binary_number = '1101'
decimal_number = int(binary_number, 2)
print(decimal_number) 输出13
```
在这里,`int`函数的第二个参数指定了输入数字的基数(2表示二进制),函数内部会根据位权原理自动计算并返回十进制结果。
四、实际应用:数字世界的桥梁
二进制到十进制的转换不仅仅是一个理论问题,它在计算机科学的多个领域都有广泛应用。
内存地址计算:在低级编程中,理解二进制到十进制的转换对于计算内存地址至关重要,因为计算机内存是按照字节(8位二进制数)分配的。
错误检测与校正:许多现代通信协议和数据存储系统利用二进制数的特性进行错误检测和校正,转换过程是这些算法实现的基础。
图像处理:数字图像由像素组成,每个像素的颜色和亮度信息通常以二进制形式存储。了解转换机制有助于图像处理算法的开发和优化。
加密算法:许多加密算法依赖于二进制数的操作和转换,如对称加密中的位运算和非对称加密中的密钥生成。
五、深化理解:从十进制到二进制的逆向思考
虽然本文聚焦于二进制到十进制的转换,但理解这一过程也有助于逆向思考,即从十进制转换回二进制。这种双向转换能力对于全面掌握数制转换至关重要。
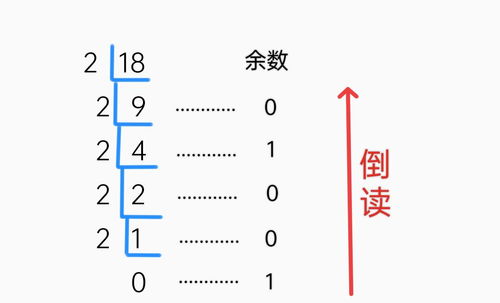
十进制转二进制通常采用“除2取余法”:将十进制数除以2,记录余数,然后将商继续除以2,直到商为0。最后,将得到的余数从下到上排列,即为对应的二进制数。例如,十进制数13转换为二进制数的过程为:13 ÷ 2 = 6 余 1,6 ÷ 2 = 3 余 0,3 ÷ 2 = 1 余 1,1 ÷ 2 = 0
- 上一篇: 掌握精髓:撰写高效教材分析的实用指南
- 下一篇: 掌握书信撰写的艺术:让你的文字温暖人心
-
 二进制如何轻松转换为十进制?资讯攻略02-28
二进制如何轻松转换为十进制?资讯攻略02-28 -
 揭秘数字魔法:轻松掌握十进制到二进制的转换秘籍资讯攻略11-04
揭秘数字魔法:轻松掌握十进制到二进制的转换秘籍资讯攻略11-04 -
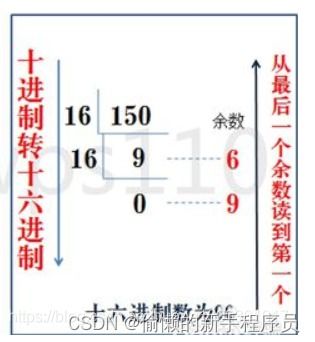 轻松掌握:16进制转10进制的方法资讯攻略02-23
轻松掌握:16进制转10进制的方法资讯攻略02-23 -
 如何将16进制转换为10进制?资讯攻略12-07
如何将16进制转换为10进制?资讯攻略12-07 -
 二进制与八进制相互转换方法资讯攻略10-28
二进制与八进制相互转换方法资讯攻略10-28 -
 解码数字奥秘:二进制与十进制互转全攻略,轻松掌握转换技巧!资讯攻略10-24
解码数字奥秘:二进制与十进制互转全攻略,轻松掌握转换技巧!资讯攻略10-24









