函数的拐点如何确定？

在数学的广袤天地中，函数作为描述变量间关系的强大工具，其形态与性质一直是研究的重点。在这众多性质之中，拐点作为函数图像上一个独特而重要的特征，不仅承载着函数变化趋势的关键信息，还深刻影响着我们对函数行为的理解和应用。拐点，简而言之，是函数图像上凹凸性发生变化的点，是函数单调性转折的标志性位置。本文将从定义解析、几何直观、微积分视角、应用实例及计算求解等多个维度，深入探索函数拐点的奥秘。

定义解析：拐点的精确界定

在数学分析中，拐点正式定义为：若函数f(x)在区间I内可导，且存在点c∈I，使得f''(c)=0（f''(x)表示f(x)的二阶导数），同时在c的两侧，f''(x)的符号相反，则称点c为函数f(x)的拐点。这一定义揭示了拐点的两个核心要素：一是二阶导数为零，二是二阶导数在这一点两侧符号相反。前者是拐点的必要条件，后者则是充分条件，二者共同确保了函数在该点由凹变凸或由凸变凹的特性。

几何直观：拐点与函数图像的视觉联系

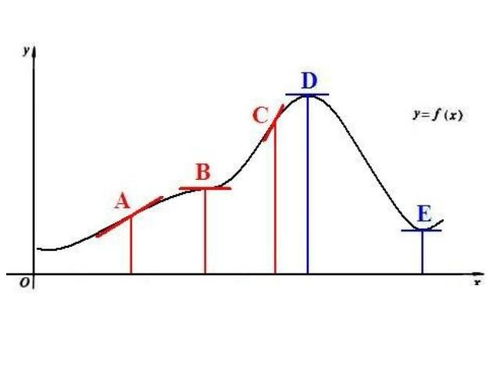
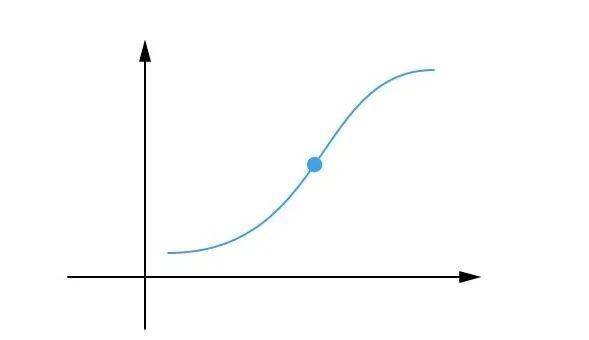
从几何图形的角度看，拐点是函数图像上一个“弯曲方向改变”的点。想象一条平滑的曲线，在拐点之前，它可能以一种方式弯曲（比如向上凸起），而在拐点之后，弯曲的方向发生了改变（比如变为向下凹陷）。这种视觉上的转折，直观地反映了函数增减速度（即一阶导数）的变化率（即二阶导数）在拐点的突变。因此，通过观察函数图像上的拐点，我们可以直观地捕捉到函数行为的重要转折点，这对于理解函数的整体趋势极为关键。

微积分视角：拐点与导数的关系

微积分是研究函数拐点不可或缺的工具。在微积分框架下，一阶导数f'(x)描述了函数f(x)在某一点的变化率，即函数图像的切线斜率；而二阶导数f''(x)则揭示了一阶导数f'(x)的变化率，即切线斜率的变化情况。因此，二阶导数的正负直接决定了函数图像的凹凸性：当f''(x)>0时，函数图像在该区间内向上凸起（凹）；当f''(x)<0时，函数图像在该区间内向下凹陷（凸）。拐点正是这两种凹凸性转换的“临界点”，也即二阶导数由正变负或由负变正的点。

应用实例：拐点在现实生活与科学中的体现

拐点的概念远不止于抽象的数学分析，它在现实生活与科学研究中有着广泛的应用。在经济学中，需求曲线或供给曲线的拐点，标志着价格与数量关系的根本变化，对制定经济政策和预测市场趋势至关重要。在物理学中，物体的运动轨迹或力-位移曲线中的拐点，揭示了物体运动状态的突变，如速度的急剧增减或加速度方向的改变。在生物学领域，种群增长曲线的拐点，预示着种群数量的增长趋势将发生逆转，对于生态保护和管理具有重要意义。此外，在金融分析、工程设计、医学诊断等领域，拐点同样扮演着重要的角色，为决策制定提供了科学依据。

计算求解：如何找到函数的拐点

寻找函数的拐点，通常需要遵循以下步骤：

1. 求一阶导数：首先，对给定的函数f(x)求一阶导数f'(x)，以了解函数的增减性。

2. 求二阶导数：接着，对一阶导数f'(x)求导，得到二阶导数f''(x)，这是判断拐点存在的关键。

3. 解方程：设置f''(x)=0，解此方程得到可能的拐点候选点。

4. 检验符号变化：对于每个候选点，检查其在f''(x)中的符号变化，确保在候选点两侧f''(x)的符号确实相反。这一步是确认拐点的关键，因为仅满足f''(x)=0而不满足符号变化条件的点，并非真正的拐点。

5. 综合分析：结合函数的定义域、一阶和二阶导数的性质，以及可能的边界条件，综合分析得出最终的拐点。

值得注意的是，某些函数可能不存在拐点，比如常数函数或线性函数，其图像是直线，没有弯曲，自然也就不存在拐点。而对于某些复杂的非线性函数，拐点的计算可能需要复杂的数学工具或数值方法。

结语

拐点，作为函数图像上一个微妙的转折点，不仅是数学分析中的一个基本概念，更是连接数学理论与现实世界的桥梁。通过对拐点的深入探索，我们不仅能够更好地理解函数的性质和行为，还能洞察到它在众多学科领域的广泛应用，从而更有效地解决实际问题。拐点的存在，不仅丰富了数学的内涵，也为人类探索自然规律、推动科技进步提供了有力的数学工具。在数学的浩瀚星空中，拐点以其独特的光芒，照亮了我们前行的道路。