什么是高等数学中的曲线拐点?如何求解拐点定义及方法
走进高等数学:揭秘曲线拐点的定义及求法

在数学的广阔世界里,高等数学犹如一座神秘的宝库,等待着我们去探索与发现。今天,让我们一起揭开高等数学中一个既基础又迷人的篇章——曲线拐点。想象一下,当你漫步在一条蜿蜒曲折的小径上,时而上坡,时而下坡,那些让你脚步方向骤变的转折点,便是我们今天要探讨的“拐点”。在数学的语境中,拐点不仅是图形上的一个点,更是函数性质变化的标志。
一、拐点的神秘面纱:定义与直观理解
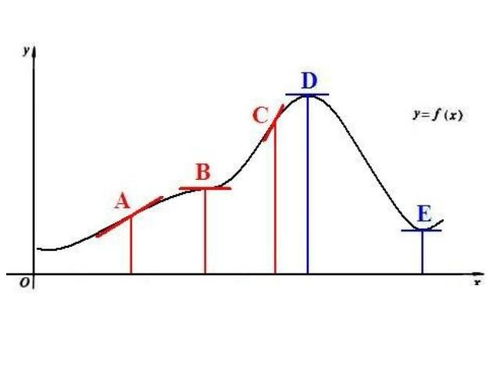
拐点,顾名思义,是曲线上一个“拐”的点。在数学上,它指的是曲线上某一点两侧的切线斜率符号发生变化的点。换句话说,如果你在曲线上沿着某一方向前进,当到达拐点时,你会发现曲线的凹凸性(或称为弯曲方向)发生了改变。这一点在视觉上非常明显,比如一条先凹后凸的曲线,其拐点就是凹与凸的分界线。
为了更直观地理解拐点,我们可以想象一个抛物线的顶点。在顶点左侧,曲线是凹向下的;而在顶点右侧,曲线则凹向上。这个顶点,实际上就是抛物线上的一个拐点,只不过对于标准的二次函数来说,它是最特别的那个点——唯一的一个拐点。但对于更复杂的函数来说,拐点可能不止一个,甚至可能根本不存在。
二、探索拐点的秘密:一阶导数与二阶导数
既然拐点是曲线上切线斜率符号发生变化的点,那么我们很自然地会想到利用导数来寻找它。导数,作为描述函数变化率的工具,在这里将发挥关键作用。但直接求一阶导数并不能直接找到拐点,因为一阶导数只能告诉我们函数在某点的切线斜率,而无法揭示斜率的变化趋势。
这时,我们需要引入二阶导数。二阶导数,即一阶导数的导数,它描述了函数斜率的变化率。换句话说,二阶导数能够告诉我们曲线在某点附近是变得更加陡峭还是更加平缓,以及这种变化的趋势是加速还是减速。
三、拐点求解大法:二阶导数测试
现在,我们已经有了寻找拐点的利器——二阶导数。那么,具体如何操作呢?
1. 求一阶导数:首先,对给定的函数求一阶导数,得到其切线斜率的表达式。
2. 求二阶导数:接着,对一阶导数再求一次导,得到二阶导数。
3. 寻找临界点:令二阶导数等于0,或者考虑二阶导数不存在的点(如分母为0的点),这些点可能是潜在的拐点。
4. 判断凹凸性:对于每个临界点,检查其左右两侧的二阶导数符号。如果符号相反,则该临界点就是拐点。
举个例子,假设我们有一个函数f(x) = x^3 - 6x^2 + 11x - 6,想找到它的拐点。
首先,求一阶导数:f'(x) = 3x^2 - 12x + 11。
然后,求二阶导数:f''(x) = 6x - 12。
接着,令二阶导数等于0:6x - 12 = 0,解得x = 2。
最后,检查x = 2两侧的二阶导数符号。当x < 2时,f''(x) < 0;当x > 2时,f''(x) > 0。因此,x = 2是一个拐点。
四、拐点的实际应用:从理论到实践
拐点不仅在理论上具有重要意义,在实际应用中也扮演着重要角色。
经济学:在经济学中,拐点常用于分析供需曲线的变化。例如,当供给曲线在某个点由上升变为下降时,这个点就是拐点,它可能预示着市场供需关系的重大变化。
工程学:在工程设计中,拐点常用于确定结构的应力分布。例如,在桥梁设计中,通过分析桥梁荷载-位移曲线的拐点,可以评估桥梁的承载能力和安全性。
物理学:在物理学中,拐点常用于描述物体的运动状态变化。例如,在抛体运动中,通过分析速度-时间曲线的拐点,可以确定物体何时达到最高点或开始下落。
五、深入探索:拐点与极值点的区别
在高等数学的学习中,拐点与极值点是两个容易混淆的概念。虽然它们都是函数性质变化的标志,但有着本质的区别。
极值点:极值点是函数在某点取得最大值或最小值的点。通过一阶导数等于0或不存在,以及二阶导数大于0(极小值点)或小于0(极大值点)来判断。
拐点:拐点则是曲线上切线斜率符号发生变化的点。通过二阶导数等于0或不存在,并检查其左右两侧的符号变化来判断。
简而言之,极值点关注的是函数值的局部最大或最小,而拐点关注的是曲线凹凸性的变化。两者在数学上各有其独特的意义和应用。
六、结语:开启高等数学之旅
通过今天的探索,我们揭开了曲线拐点的神秘面纱,从定义到求解方法,再到实际应用和与极值点的区别,都进行了详细的阐述。拐点作为高等数学中的一个重要概念,不仅在数学理论中占据重要地位,也在实际应用中发挥着重要作用。
高等数学的世界充满了无尽的奥秘和魅力,拐点只是其中冰山一角。未来,我们将继续探索这座宝库,发现更多令人惊叹的数学之美。让我们一起,怀揣着对知识的渴望和对未知的好奇,踏上这段充满挑战与乐趣的高等数学之旅吧!
- 上一篇: 揭秘:如何查看QQ中谁对你设置了特别关心?
- 下一篇: 家常美味秘籍:菜花炒肉的制作绝招
-
 揭秘:拐点究竟是指一个点还是坐标?资讯攻略12-02
揭秘:拐点究竟是指一个点还是坐标?资讯攻略12-02 -
 函数的拐点如何确定?资讯攻略11-22
函数的拐点如何确定?资讯攻略11-22 -
 双曲线的顶点坐标公式及求解方法资讯攻略10-28
双曲线的顶点坐标公式及求解方法资讯攻略10-28 -
 高等数学入门:你了解全微分方程的概念及其解法吗?资讯攻略02-27
高等数学入门:你了解全微分方程的概念及其解法吗?资讯攻略02-27 -
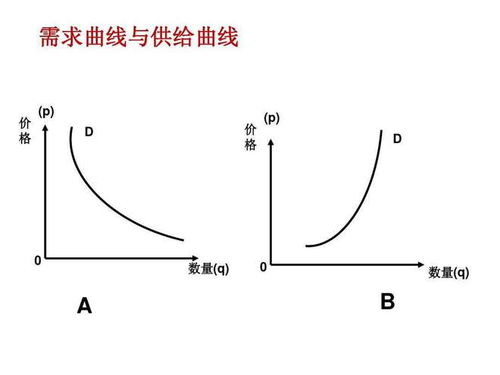 需求曲线与供给曲线的定义及区分方法资讯攻略12-02
需求曲线与供给曲线的定义及区分方法资讯攻略12-02 -
 cot导数的定义与计算方法资讯攻略11-24
cot导数的定义与计算方法资讯攻略11-24












