指数函数有哪8个基本公式?
指数函数的八个基本公式详解

在数学的广阔领域中,指数函数以其独特的性质和广泛的应用性占据了重要地位。无论是科学研究、工程技术还是经济学等领域,指数函数都扮演着不可或缺的角色。为了帮助大家更好地理解和掌握这一函数类型,本文将详细介绍指数函数的八个基本公式。

一、指数函数的基本定义

首先,我们需要明确指数函数的基本定义。一般地,形如y=a^x(a>0且a≠1,x为实数)的函数被称为指数函数。其中,a被称为底数,x被称为指数。指数函数描绘了底数a经过x次幂运算后的结果。
二、指数函数的运算性质
1. a^m×a^n=a^(m+n) (同底数幂相乘,底数不变,指数相加)
这是指数函数的一个基本运算性质。当两个指数函数具有相同的底数时,它们的乘积可以通过将各自的指数相加来求得。例如,a^2×a^3=a^(2+3)=a^5。这一性质在简化复杂表达式和进行数学运算时非常有用。
2. a^m÷a^n=a^(m-n) (同底数幂相除,底数不变,指数相减)
与乘法性质类似,当两个指数函数具有相同的底数时,它们的商可以通过将各自的指数相减来求得。例如,a^5÷a^2=a^(5-2)=a^3。这一性质在求解包含指数函数的除法问题时非常便捷。
3. (a^m)^n=a^(m×n) (幂的乘方,底数不变,指数相乘)
当一个指数函数的幂再次被求幂时,可以通过将这两个幂的指数相乘来求得结果。例如,(a^2)^3=a^(2×3)=a^6。这一性质在处理复杂的幂运算时非常有用。
4. a^(-n)=1/(a^n) (负整数指数幂的定义)
负整数指数幂的定义是指数函数的一个重要组成部分。当一个指数函数的指数为负数时,可以通过取该指数函数的倒数并将其指数变为正数来求得结果。例如,a^(-3)=1/(a^3)。这一性质在处理包含负指数的指数函数时非常关键。
5. a^0=1(零指数幂的定义)
任何非零数的零次幂都等于1,这是指数函数的一个基本定义。例如,a^0=1(其中a≠0)。这一性质在简化包含零指数的指数函数时非常有用。
三、指数函数的换底公式及性质
6. log_a(N)=log_b(N)/log_b(a) (换底公式)
换底公式是指数函数和对数函数之间的重要桥梁。它允许我们将一个以a为底的对数转换为以b为底的对数,从而方便地利用不同底数的对数进行计算。例如,如果我们想要求解log_2(8),可以利用换底公式将其转换为log_10(8)/log_10(2),从而利用常用对数表或计算器进行求解。
7. log_a(M^n)=n*log_a(M) (对数的幂运算法则)
对数的幂运算法则允许我们将一个幂的对数分解为幂的指数与底数的对数的乘积。例如,log_2(8)=log_2(2^3)=3*log_2(2)=3。这一性质在简化包含幂的对数表达式时非常有用。
8. log_a(M/N)=log_a(M)-log_a(N) (对数的除法运算法则)
对数的除法运算法则允许我们将一个商的对数分解为被除数的对数与除数的对数的差。例如,log_2(4/2)=log_2(4)-log_2(2)=2-1=1。这一性质在简化包含商的对数表达式时非常便捷。
四、指数函数的应用实例
指数函数在现实生活中的应用非常广泛。例如,在人口增长、放射性衰变、利息计算等方面,指数函数都发挥着重要作用。
1. 人口增长:在人口增长问题中,指数函数可以用来描述人口随时间的变化规律。假设初始人口为P0,年增长率为r,则经过t年后的人口数量可以表示为P=P0×(1+r)^t。
2. 放射性衰变:在放射性衰变问题中,指数函数可以用来描述放射性物质随时间的变化规律。假设初始放射性物质的质量为m0,半衰期为T,则经过t时间后的放射性物质的质量可以表示为m=m0×(1/2)^(t/T)。
3. 利息计算:在利息计算问题中,指数函数可以用来描述本金随时间的变化规律。假设初始本金为P0,年利率为r(以小数形式表示),则经过t年后的本金(包括利息)可以表示为A=P0×(1+r)^t。
五、总结
通过本文的介绍,我们了解了指数函数的八个基本公式及其运算性质。这些公式和性质不仅在数学领域具有广泛的应用价值,而且在物理学、化学、生物学等自然科学领域以及经济学、金融学等社会科学领域也发挥着重要作用。因此,掌握这些公式和性质对于提高我们的数学素养和解决实际问题能力具有重要意义。
在学习和应用这些公式时,我们需要注意以下几点:首先,要准确理解每个公式的含义和适用范围;其次,要熟练掌握这些公式的运算方法和技巧;最后,要善于运用这些公式解决实际问题,并在实践中不断巩固和深化对这些公式的理解和掌握。
-
 幂运算必备:解锁八大核心公式!资讯攻略11-09
幂运算必备:解锁八大核心公式!资讯攻略11-09 -
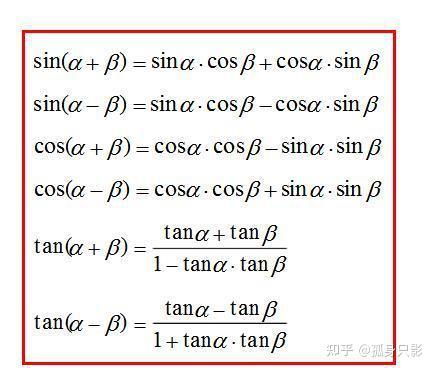 掌握三角函数公式,轻松解题无压力!资讯攻略11-28
掌握三角函数公式,轻松解题无压力!资讯攻略11-28 -
 高中数学必备:三角函数公式全集(终极版)资讯攻略11-30
高中数学必备:三角函数公式全集(终极版)资讯攻略11-30 -
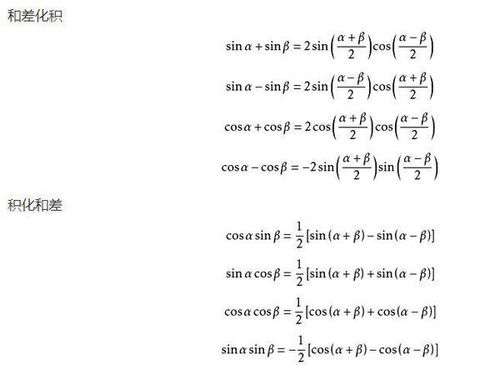 掌握常见三角函数积分公式:推导技巧与全面总结资讯攻略11-19
掌握常见三角函数积分公式:推导技巧与全面总结资讯攻略11-19 -
 Excel中绝对值函数的优化使用公式资讯攻略11-03
Excel中绝对值函数的优化使用公式资讯攻略11-03 -
 Excel中如何进行减法运算的函数公式资讯攻略11-19
Excel中如何进行减法运算的函数公式资讯攻略11-19