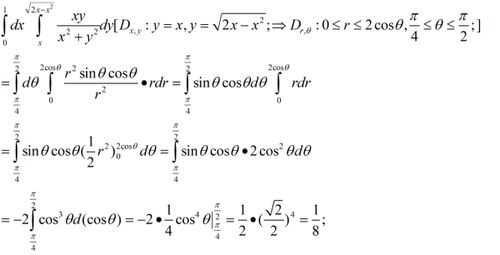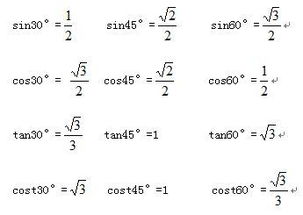掌握常见三角函数积分公式:推导技巧与全面总结
常见三角函数积分公式的推导与总结
在微积分的学习中,三角函数积分公式占据了极其重要的地位。它们不仅广泛应用于物理学、工程学等领域,而且是学习更高阶数学的基础。本文将详细推导和总结常见的三角函数积分公式,以便读者能够更深入地理解和应用这些公式。

一、正弦函数和余弦函数的积分

正弦函数和余弦函数是最基本的三角函数,它们的积分公式也最为基础。
1. 正弦函数的积分
∫sin(x)dx = -cos(x) + C
推导过程:
我们知道三角恒等式d(cos(x))/dx = -sin(x),根据微积分基本定理,对等式两边同时积分,得到
∫-sin(x)dx = cos(x) + C
移项得到
∫sin(x)dx = -cos(x) + C
2. 余弦函数的积分
∫cos(x)dx = sin(x) + C
推导过程:
同样地,我们知道三角恒等式d(sin(x))/dx = cos(x),根据微积分基本定理,对等式两边同时积分,得到
∫cos(x)dx = sin(x) + C
二、正切函数和余切函数的积分
正切函数和余切函数可以看作是正弦函数和余弦函数的比值,因此它们的积分相对复杂一些。
1. 正切函数的积分
∫tan(x)dx = -ln|cos(x)| + C
推导过程:
首先,我们知道tan(x) = sin(x)/cos(x),所以
∫tan(x)dx = ∫(sin(x)/cos(x))dx
使用u-substitution方法,令u = cos(x),则du = -sin(x)dx,代入得到
∫tan(x)dx = -∫(1/u)du = -ln|u| + C = -ln|cos(x)| + C
2. 余切函数的积分
∫cot(x)dx = ln|sin(x)| + C
推导过程:
同样地,我们知道cot(x) = cos(x)/sin(x),所以
∫cot(x)dx = ∫(cos(x)/sin(x))dx
使用u-substitution方法,令u = sin(x),则du = cos(x)dx,代入得到
∫cot(x)dx = ∫(1/u)du = ln|u| + C = ln|sin(x)| + C
三、正割函数和余割函数的积分
正割函数和余割函数分别是正切函数和余切函数的倒数,它们的积分更加复杂。
1. 正割函数的积分
∫sec(x)dx = ln|sec(x) + tan(x)| + C
推导过程:
首先,我们知道sec(x) = 1/cos(x),所以
∫sec(x)dx = ∫(1/cos(x))dx
使用三角恒等式sec^2(x) = 1 + tan^2(x),得到
∫sec(x)dx = ∫sec^2(x)/sec(x)dx = ∫(1 + tan^2(x))/sec(x)dx
令u = tan(x),则du = sec^2(x)dx,代入得到
∫sec(x)dx = ∫(1 + u^2)/(u^2 + 1)du/sec(x) = ∫du/sec(x)
由于sec(x) = sqrt(1 + tan^2(x)) = sqrt(1 + u^2),所以
∫sec(x)dx = ∫du/sqrt(1 + u^2) = ln|u + sqrt(1 + u^2)| + C
将u = tan(x)代回,得到
∫sec(x)dx = ln|tan(x) + sqrt(1 + tan^2(x))| + C = ln|sec(x) + tan(x)| + C
2. 余割函数的积分
∫csc(x)dx = ln|csc(x) - cot(x)| + C
推导过程:
首先,我们知道csc(x) = 1/sin(x),所以
∫csc(x)dx = ∫(1/sin(x))dx
使用三角恒等式csc^2(x) = 1 + cot^2(x),得到
∫csc(x)dx = ∫csc^2(x)/csc(x)dx = ∫(1 + cot^2(x))/csc(x)dx
令u = cot(x),则du = -csc^2(x)dx,代入得到
∫csc(x)dx = -∫(1 + u^2)/(u^2 + 1)du/csc(x) = -∫du/csc(x)
由于csc(x) = sqrt(1 + cot^2(x)) = sqrt(1 + u^2),所以
∫csc(x)dx = -∫du/sqrt(1 + u^2) = -ln|u + sqrt(1 + u^2)| + C
但注意到这里我们需要一个正号,因为原式是∫csc(x)dx,而不是-∫csc(x)dx。所以我们可以将结果写为
∫csc(x)dx = ln|(-u - sqrt(1 + u^2))/(-1)| + C = ln|csc(x) + cot(x)| - ln|-1| + C = ln|csc(x) - cot(x)| + C
(注意:这里我们利用了ln|a/b| = ln|a| - ln|b|的性质,并且因为C是任意常数,所以-ln|-1|可以吸收到C中)
四、总结
以上我们推导了常见的三角函数积分公式,包括正弦函数、余弦函数、正切函数、余切函数、正割函数和余割函数的积分。这些公式在学习微积分的过程中非常重要,它们不仅可以直接用于求解相关积分问题,还可以作为推导其他复杂积分公式的基础。希望读者能够熟练掌握这些公式,并在实际应用中灵活运用它们。
- 上一篇: 2024年315晚会回放,精彩内容不容错过的观看指南!
- 下一篇: 如何创建自己的YY频道
-
 积分学的基石:深入探索基本公式资讯攻略02-14
积分学的基石:深入探索基本公式资讯攻略02-14 -
 全面掌握!24个必备二重积分公式精选集资讯攻略01-18
全面掌握!24个必备二重积分公式精选集资讯攻略01-18 -
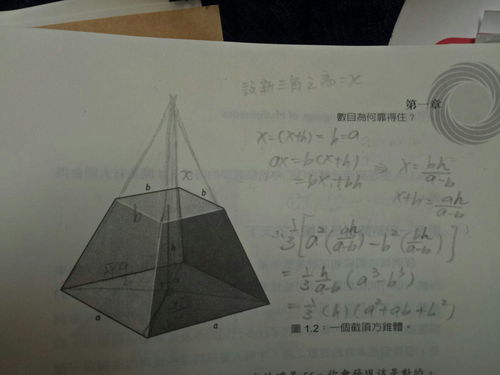 棱锥体积公式详解,轻松掌握!资讯攻略10-30
棱锥体积公式详解,轻松掌握!资讯攻略10-30 -
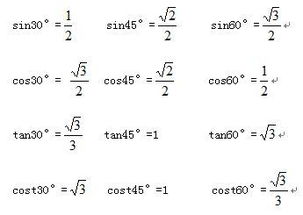 三角函数常见公式都有哪些?资讯攻略11-28
三角函数常见公式都有哪些?资讯攻略11-28 -
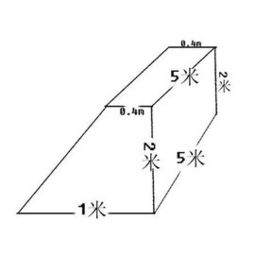 揭秘梯形体积计算的神秘公式!资讯攻略11-10
揭秘梯形体积计算的神秘公式!资讯攻略11-10 -
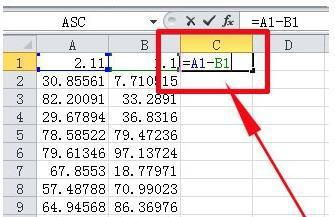 Excel中轻松掌握减法函数的实用技巧资讯攻略11-18
Excel中轻松掌握减法函数的实用技巧资讯攻略11-18