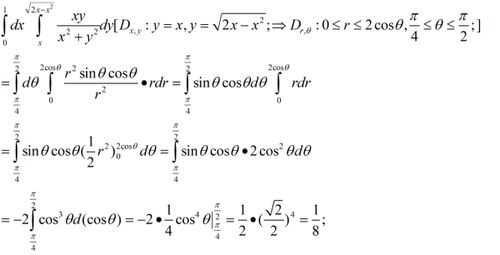高中数学必备:三角函数公式全集(终极版)
高中数学三角函数公式详解

三角函数是高中数学中极为重要的一部分,广泛应用于解题和实际问题解决中。为了帮助广大考生系统地掌握三角函数公式,本文整理了最全面、最详细的三角函数公式集合,希望能对考生们的备考之路有所帮助。

一、基本三角函数定义
三角函数是基于直角三角形边长比值定义的,主要包括正弦(sin)、余弦(cos)、正切(tan)三种基本函数,以及它们的倒数、平方、和差等派生函数。

1. 正弦函数:sin(α) = 对边 / 斜边

2. 余弦函数:cos(α) = 邻边 / 斜边

3. 正切函数:tan(α) = 对边 / 邻边
二、诱导公式
利用诱导公式,可以将任意角度的三角函数值转化为已知角度的三角函数值,极大地简化了计算。
1. 奇变偶不变,符号看象限:
sin(π/2 - α) = cos(α)
cos(π/2 - α) = sin(α)
tan(π/2 - α) = cot(α)
sin(π/2 + α) = cos(α)(符号相反)
cos(π/2 + α) = -sin(α)
tan(π/2 + α) = -cot(α)
sin(π - α) = sin(α)(符号不变)
cos(π - α) = -cos(α)
tan(π - α) = -tan(α)
sin(π + α) = -sin(α)(符号相反)
cos(π + α) = -cos(α)
tan(π + α) = tan(α)
sin(3π/2 - α) = -cos(α)
cos(3π/2 - α) = -sin(α)
tan(3π/2 - α) = tan(α)
sin(3π/2 + α) = -cos(α)(符号不变)
cos(3π/2 + α) = sin(α)
tan(3π/2 + α) = -cot(α)
三、两角和与差公式
两角和与差公式是三角函数的重要公式,它们将两个角度的三角函数值转化为单个角度的三角函数值。
1. 两角和公式:
sin(α + β) = sinαcosβ + cosαsinβ
cos(α + β) = cosαcosβ - sinαsinβ
tan(α + β) = (tanα + tanβ) / (1 - tanαtanβ)
2. 两角差公式:
sin(α - β) = sinαcosβ - cosαsinβ
cos(α - β) = cosαcosβ + sinαsinβ
tan(α - β) = (tanα - tanβ) / (1 + tanαtanβ)
四、二倍角公式
二倍角公式可以将一个角度的二倍角的三角函数值用单个角度的三角函数值表示。
1. 正弦公式:sin2α = 2sinαcosα
2. 余弦公式:cos2α = cos²α - sin²α = 1 - 2sin²α = 2cos²α - 1
3. 正切公式:tan2α = (2tanα) / (1 - tan²α)
五、半角公式
半角公式可以将一个角度的一半角的三角函数值用该角度的三角函数值表示。
1. 正弦公式:sin(α/2) = ±√[(1 - cosα) / 2]
2. 余弦公式:cos(α/2) = ±√[(1 + cosα) / 2]
3. 正切公式:tan(α/2) = ±√[(1 - cosα) / (1 + cosα)] = (1 - cosα) / sinα = sinα / (1 + cosα)
六、万能公式
万能公式将三角函数值转化为tan(α/2)的函数,常用于求解复杂三角函数问题。
1. 正弦公式:sinα = 2tan(α/2) / [1 + tan²(α/2)]
2. 余弦公式:cosα = [1 - tan²(α/2)] / [1 + tan²(α/2)]
3. 正切公式:tanα = [2tan(α/2)] / [1 - tan²(α/2)]
七、和差化积公式
和差化积公式可以将两个角度的和或差的三角函数值转化为积的形式,常用于化简和求解三角函数表达式。
1. 正弦公式:sinα + sinβ = 2sin[(α + β) / 2]cos[(α - β) / 2]
sinα - sinβ = 2cos[(α + β) / 2]sin[(α - β) / 2]
2. 余弦公式:cosα + cosβ = 2cos[(α + β) / 2]cos[(α - β) / 2]
cosα - cosβ = -2sin[(α + β) / 2]sin[(α - β) / 2]
3. 正切公式:tanα + tanβ = (tanα + tanβ)(1 - tanαtanβ) / (1 - tanαtanβ) = tan(α + β)(1 - tanαtanβ)
tanα - tanβ = (tanα - tanβ)(1 + tanαtanβ) / (1 + tanαtanβ) = tan(α - β)(1 + tanαtanβ)
八、积化和差公式
积化和差公式可以将两个角度的三角函数值的积转化为和或差的形式,同样常用于化简和求解三角函数表达式。
1. 正弦公式:sinαsinβ = -1/2[cos(α + β) - cos(α - β)]
2. 余弦公式:cosαcosβ = 1/2[cos(α + β) + cos(α - β)]
3. 正切公式:sinαcosβ = 1/2[sin(α + β) + sin(α - β)]
cosαsinβ = 1/2[sin(α + β) - sin(α - β)]
九、辅助角公式
辅助角公式常用于将复杂的三角函数表达式化简为单一的三角函数形式,便于求解。
1. 正弦型公式:a*sinα + b*cosα = √(a² + b²)sin(α + φ)(其中,tanφ = b / a)
2. 余弦型公式:a*sinα - b*cosα = √(a² + b²)cos(α - φ)(其中,tanφ = a / b)
十、反三角函数
反三角函数是三角函数的反函数,用于求解三角方程中的未知角。
1. 反正弦函数:arcsin(x)
2. 反余弦函数:arccos(x)
3. 反正切函数:arctan(x)
4. 反余切函数:arccot(x)
结语
三角函数公式众多,但掌握它们并非难事。通过不断练习和应用,考生们可以逐渐熟悉并灵活运用这些公式,提高解题速度和准确性。希望本文提供的三角函数公式大全能为考生们的备考之路提供帮助,祝大家在考试中取得优异成绩!
-
 高中数学:轻松掌握扇形弧长和面积公式资讯攻略11-08
高中数学:轻松掌握扇形弧长和面积公式资讯攻略11-08 -
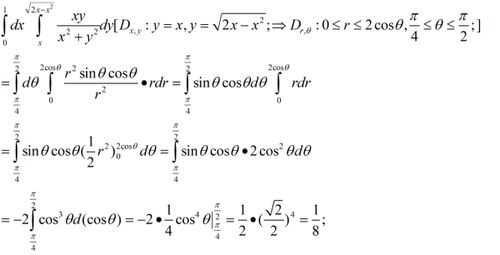 全面掌握!24个必备二重积分公式精选集资讯攻略01-18
全面掌握!24个必备二重积分公式精选集资讯攻略01-18 -
 揭秘:二阶微分方程的3种必备通解公式资讯攻略11-22
揭秘:二阶微分方程的3种必备通解公式资讯攻略11-22 -
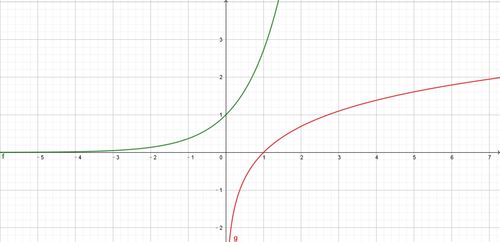 掌握log函数求导公式,轻松解决数学问题资讯攻略11-09
掌握log函数求导公式,轻松解决数学问题资讯攻略11-09 -
 三角函数cot的定义及公式是什么?资讯攻略11-24
三角函数cot的定义及公式是什么?资讯攻略11-24 -
 水树奈奈解析幂函数公式,轻松掌握数学要点资讯攻略11-09
水树奈奈解析幂函数公式,轻松掌握数学要点资讯攻略11-09