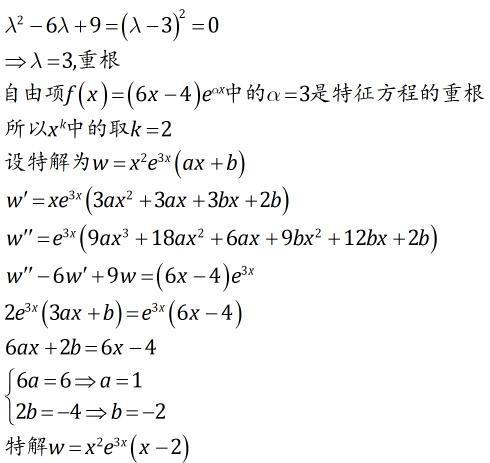揭秘:二阶微分方程的3种必备通解公式
二阶微分方程的3种通解公式

二阶微分方程是数学中的一个重要概念,用于描述函数的二阶导数与其自变量及函数本身之间的关系。其一般形式可以表示为a(x)y'' + b(x)y' + c(x)y = f(x),其中a(x), b(x), c(x)为系数函数,f(x)为非齐次项。根据f(x)的值,二阶微分方程可以分为齐次方程(f(x)=0)和非齐次方程(f(x)≠0)。本文将从这两种情况出发,详细介绍二阶微分方程的三种通解公式。

齐次方程通解公式
齐次方程是指f(x)=0时的二阶微分方程,即a(x)y'' + b(x)y' + c(x)y = 0。对于常系数齐次方程,即a(x), b(x), c(x)均为常数时,其通解公式可以根据特征方程的根的情况来确定。

1. 特征根为不相等实数r1和r2时

当特征方程ar^2 + br + c = 0有两个不相等的实数根r1和r2时,齐次方程的通解为:
y = C1e^(r1x) + C2e^(r2x)
其中,C1和C2是任意常数。这一公式表明,齐次方程的解可以表示为两个指数函数的线性组合。
2. 特征根为相等实数r时
当特征方程ar^2 + br + c = 0有两个相等的实数根r时,齐次方程的通解为:
y = (C1 + C2x)e^(rx)
其中,C1和C2是任意常数。这一公式表明,当特征根相等时,齐次方程的解中除了一个指数函数外,还需要乘以一个线性函数来确保解的线性无关性。
3. 特征根为共轭复数时
当特征方程ar^2 + br + c = 0有一对共轭复数根r = α±βi时,齐次方程的通解为:
y = C1e^(αx)cos(βx) + C2e^(αx)sin(βx)
其中,C1和C2是任意常数。这一公式表明,当特征根为共轭复数时,齐次方程的解可以表示为两个指数函数与余弦函数和正弦函数的乘积的线性组合。
非齐次方程通解公式
非齐次方程是指f(x)≠0时的二阶微分方程。对于非齐次方程,其通解可以由齐次方程的通解和非齐次方程的一个特解组成。
通解公式:y = yh + yp
其中,yh是齐次方程的通解,yp是非齐次方程的一个特解。
1. 齐次方程的通解yh
齐次方程的通解yh可以根据上述齐次方程通解公式求得,即根据特征方程的根的情况来确定。
2. 非齐次方程的特解yp
非齐次方程的特解yp的求解方法取决于f(x)的形式。常用的方法包括待定系数法和常数变易法。
待定系数法:如果f(x)是多项式、指数函数、正弦函数或余弦函数,或者它们的线性组合,则可以假设特解具有与f(x)相似的形式,然后代入原方程求解待定系数。
常数变易法:对于更一般的f(x),可以使用常数变易法。该方法将特解表示为y_p = u1(x)y1(x) + u2(x)y2(x),其中y1(x)和y2(x)是齐次方程的两个线性无关的解,u1(x)和u2(x)通过求解一个线性方程组确定。
应用举例
二阶微分方程在物理学、工程学等领域有着广泛的应用。以下是一些具体的应用举例。
1. 物理问题中的应用
在物理学中,二阶微分方程常用于描述振动和波动等现象。例如,简谐振动的运动方程就是一个二阶微分方程,通过求解这个方程,可以得到振动的位移、速度和加速度等物理量。此外,波动方程也是二阶微分方程的一个重要应用,它描述了波的传播规律和特性。
2. 工程学中的应用
在工程学中,二阶微分方程同样有着广泛的应用。在结构设计中,通过求解二阶微分方程,可以分析结构的受力情况和稳定性;在控制系统中,二阶微分方程可以用于描述系统的动态特性和响应速度。
3. 初值问题的求解
二阶微分方程初值问题是指给定初始条件(如y(0)和y'(0)的值)的情况下,求解二阶微分方程的问题。对于这类问题,通常需要先求出方程的通解,然后根据初始条件确定通解中的常数项,从而得到特解。初值问题的求解是二阶微分方程应用中的一个重要方面,它对于理解系统的动态行为和预测未来状态具有重要意义。
总结
二阶微分方程的通解公式取决于方程的类型(齐次或非齐次)以及特征方程的根的情况。对于齐次方程,通解形式为指数函数的线性组合(当特征根为不相等实数时)、指数函数与线性函数的乘积(当特征根相等时)或指数函数与余弦函数和正弦函数的乘积的线性组合(当特征根为共轭复数时)。对于非齐次方程,通解为齐次方程的通解加上非齐次方程的一个特解。这些通解公式为求解二阶微分方程提供了有效的数学工具,广泛应用于物理学、工程学等领域。
- 上一篇: 如何更改《淘宝》账号用户名
- 下一篇: 棒子面粥怎么熬制?
-
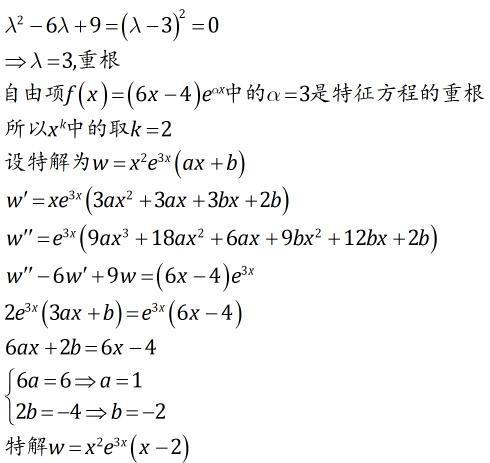 常微分方程的通解表达式是什么资讯攻略12-06
常微分方程的通解表达式是什么资讯攻略12-06 -
 揭秘麦克斯韦方程组:公式与深远意义解析资讯攻略11-20
揭秘麦克斯韦方程组:公式与深远意义解析资讯攻略11-20 -
 一阶线性微分方程公式详解资讯攻略12-06
一阶线性微分方程公式详解资讯攻略12-06 -
 如何求解一元二次方程的四种方法是什么?资讯攻略11-09
如何求解一元二次方程的四种方法是什么?资讯攻略11-09 -
 幂运算必备:解锁八大核心公式!资讯攻略11-09
幂运算必备:解锁八大核心公式!资讯攻略11-09 -
 掌握一元二次方程公式法的轻松解题步骤资讯攻略01-05
掌握一元二次方程公式法的轻松解题步骤资讯攻略01-05