常微分方程的通解表达式是什么

常微分方程通解公式揭秘：走进数学的奇妙世界

在数学这个包罗万象的领域里，常微分方程如同一座桥梁，连接着自然界和数学理论。它不仅能帮助我们理解许多物理现象，还能为工程师、物理学家、经济学家等多种学科提供强大的数学工具。而今天，我们就来聊聊这座桥梁上的“通行证”——常微分方程通解公式。它到底是什么？如何使用？又能带我们走多远呢？

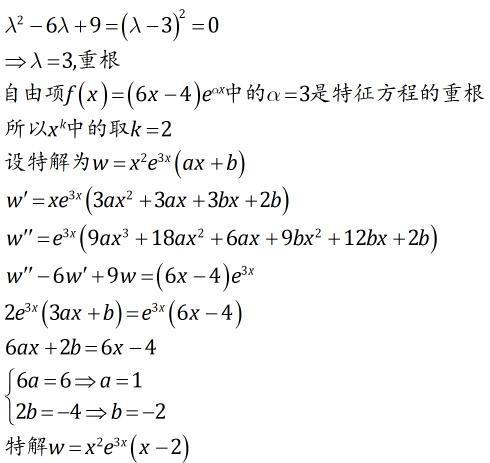
一、什么是常微分方程？

要讲通解公式，先得了解什么是常微分方程。简单来说，常微分方程就是一个包含一个或多个未知函数的方程，这些未知函数的导数（或者说变化率）会在方程中出现，而且方程中不包含关于未知函数的偏导数。用数学语言描述，如果一个方程的形式为F(x, y, y', y'', ... yn) = 0，其中y是x的未知函数，y', y'', ... yn分别表示y的一阶、二阶……n阶导数，那么这个方程就是常微分方程。

举个简单的例子，比如速度和时间的关系。如果我们知道一个物体的加速度是恒定的，那么就可以写出一个形如y'' = c（c为常数）的方程，其中y代表物体的位移，y''则是加速度。这就是一个二阶常微分方程。

二、为什么要找通解公式？

对于常微分方程，我们最关心的是找到它的解，也就是找出未知函数y(x)的具体形式。然而，大多数时候，方程的解并不唯一，而是有无穷多个，这些解构成一个解的集合，我们称之为方程的通解。而找到这个通解的过程，就需要用到通解公式。

通解公式可以帮助我们一次性地找出所有可能的解，而不必逐个试探。它不仅大大提高了解题效率，还能让我们对方程的解有更全面、更深入的理解。

三、常微分方程通解公式揭秘

不同类型的常微分方程有不同的通解公式。这里，我们介绍几种常见的类型及其通解公式。

1. 一阶线性微分方程

一阶线性微分方程是形如y' + P(x)y = Q(x)的方程，其中P(x)和Q(x)都是x的函数。这种方程的通解公式是：

y = e^(-∫P(x)dx) [∫Q(x)e^(∫P(x)dx)dx + C]

这里的C是积分常数，∫表示积分运算。这个公式看起来很复杂，但其实它的推导过程并不难理解，主要是通过乘上一个“积分因子”e^(∫P(x)dx)，将原方程转化为一个更易解的形式。

2. 二阶常系数线性微分方程

二阶常系数线性微分方程是形如y'' + ay' + by = 0的方程，其中a和b都是常数。这种方程的通解公式取决于它的特征根λ1和λ2。

如果λ1 ≠ λ2，那么通解为y = C1e^(λ1x) + C2e^(λ2x)；

如果λ1 = λ2 = λ，那么通解为y = (C1 + C2x)e^(λx)；

如果方程没有实数根，而是有一对共轭复数根α ± βi，那么通解为y = e^(αx)(C1cosβx + C2sinβx)。

这里的C1和C2同样是积分常数。

3. 一阶齐次线性微分方程组

当我们面对的是一个微分方程组，比如{y1' = P1(x)y1 + P2(x)y2, y2' = Q1(x)y1 + Q2(x)y2}时，求解会变得更加复杂。但幸运的是，对于一阶齐次线性微分方程组，我们依然可以找到通解公式。这通常涉及到矩阵和行列式的知识，其通解形式一般为Y = Ce^(AX)，其中Y是未知函数向量，C是常数向量，A是系数矩阵，X是x的向量表示，而e^(AX)则是一个矩阵指数函数。

四、如何应用通解公式？

应用通解公式解常微分方程时，通常有几个步骤：

1. 识别方程类型：首先，需要判断方程是一阶还是二阶，是线性还是非线性，是否齐次等。这一步对后续步骤至关重要。

2. 寻找或构建通解公式：根据方程的类型，选择或构建相应的通解公式。

3. 代入和求解：将方程中的系数和函数代入通解公式，通过积分、解代数方程等手段求解出未知常数。

4. 验证解：最后，将求得的解代入原方程进行验证，确保它是方程的解。

五、通解公式的局限性和扩展

虽然通解公式为我们提供了强大的工具来求解常微分方程，但它也有一定的局限性。比如，对于某些非线性方程或高阶方程，我们可能无法找到简洁的通解公式。此外，即使找到了通解公式，计算过程也可能非常复杂，甚至无法手工完成。

为了解决这些问题，数学家们开发了许多数值方法和近似方法，如欧拉法、龙格-库塔法等。这些方法可以在计算机上实现，为我们求解复杂方程提供了另一种途径。

六、结语

常微分方程通解公式是数学中的一个重要工具，它不仅能帮助我们求解方程，还能让我们对自然界的许多现象有更深入的理解。从一阶线性方程到二阶常系数方程，再到一阶齐次线性微分方程组，通解公式种类繁多，应用广泛。然而，它也并非万能，对于某些复杂方程，我们可能需要借助其他方法来求解。无论如何，学习和掌握这些通解公式，都将是我们走进数学奇妙世界的重要一步。