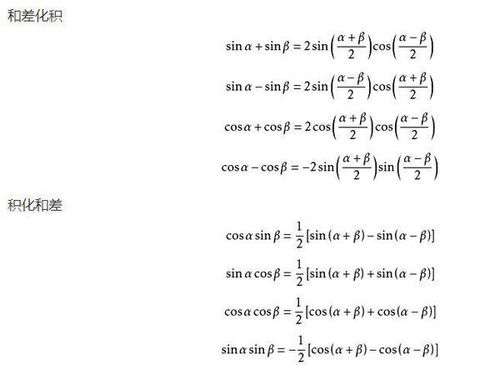等比数列求和公式是如何推导出来的?
在数学领域中,等比数列是一个重要的概念,广泛应用于金融、物理、工程等多个学科。等比数列是指从第二项起,每一项与它的前一项的比值等于同一个常数的一种数列。这个常数被称为等比数列的公比。等比数列求和公式则是解决这类数列求和问题的重要工具。本文将详细介绍等比数列求和公式的推导方法,帮助读者深入理解这一数学原理。

首先,我们回顾一下等比数列的基本性质。设等比数列的首项为a1,公比为r,则该数列可以表示为a1, a1r, a1r^2, a1r^3, ...。等比数列的通项公式为an = a1r^(n-1),其中n为项数。
接下来,我们考虑等比数列的求和问题。设等比数列的前n项和为Sn,即
Sn = a1 + a1r + a1r^2 + ... + a1r^(n-1)
我们的目标是找到Sn的表达式,即等比数列求和公式。
为了推导这个公式,我们采用一种称为“错位相减法”的技巧。首先,我们将Sn的表达式两边同时乘以公比r,得到
rSn = a1r + a1r^2 + a1r^3 + ... + a1r^n
然后,我们将原始表达式Sn与乘以r后的表达式rSn进行错位相减,即Sn - rSn,得到
(1 - r)Sn = a1 - a1r^n
这个步骤是推导过程中的关键,通过错位相减,我们消除了等比数列中的大部分项,只留下了首项a1和末项a1r^n,以及一个公因子(1 - r)。
接下来,我们对上式进行整理,解出Sn,得到
Sn = a1(1 - r^n) / (1 - r) (r ≠ 1)
这就是等比数列求和公式的基本形式。需要注意的是,这个公式在r ≠ 1时成立。当r = 1时,等比数列变为等差数列(每项都相等),此时求和公式变为Sn = na1。
为了更直观地理解这个公式的推导过程,我们可以通过一个具体的例子来进行说明。
例如,考虑等比数列1, 2, 4, 8, 16(首项a1 = 1,公比r = 2),我们要求这个数列的前5项和S5。
首先,根据等比数列求和公式,我们有
S5 = a1(1 - r^5) / (1 - r)
将a1 = 1和r = 2代入公式,得到
S5 = 1(1 - 2^5) / (1 - 2) = 1(1 - 32) / (-1) = -31 / (-1) = 31
所以,等比数列1, 2, 4, 8, 16的前5项和为31。
此外,我们还可以从另一个角度来理解等比数列求和公式的推导过程,即利用无限等比数列求和的极限思想。虽然这在本文的有限项求和公式推导中不是直接相关,但它有助于我们更深入地理解等比数列求和的本质。
无限等比数列求和公式为S = a1 / (1 - r),其中a1为首项,r为公比,且|r| < 1以保证数列的和存在且有限。这个公式可以通过将有限项求和公式中的n取极限n → ∞来得到。当n趋向于无穷大时,r^n趋向于0(|r| < 1的条件下),因此有限项求和公式中的-a1r^n项可以忽略不计,从而得到无限等比数列求和公式。
然而,需要注意的是,无限等比数列求和公式只适用于|r| < 1的情况。当|r| ≥ 1时,数列的和将趋向于无穷大或不存在,因此不能使用这个公式。
回到有限项求和的问题上来,我们还需要注意一些特殊情况的处理。例如,当r = -1且n为偶数时,等比数列的求和会出现特殊的情况。这是因为此时数列中的项会两两抵消,导致和为0(如果首项a1不为0的话)。例如,等比数列1, -1, 1, -1, ...(首项a1 = 1,公比r = -1)的前4项和为0。
另外,当n = 1时(即只考虑数列的第一项),等比数列求和公式也退化为S1 = a1,因为此时没有其他的项需要相加。
综上所述,等比数列求和公式的推导方法主要依赖于错位相减法的技巧。通过这种方法,我们可以找到等比数列前n项和的表达式。同时,我们还需要注意特殊情况的处理,如r = 1时数列变为等差数列的情况、r = -1且n为偶数时数列和为0的情况等。通过深入理解这些特殊情况,我们可以更全面地掌握等比数列求和公式的应用。
在数学学习和应用中,等比数列求和公式是一个非常重要的工具。它不仅可以用于解决等比数列的求和问题,还可以与其他数学知识相结合,解决更复杂的数学问题。因此,熟练掌握等比数列求和公式的推导方法和应用技巧,对于提高数学素养和解决实际问题具有重要意义。
- 上一篇: 揭秘!中江省绿藤市究竟隐藏在中国的哪个省份?
- 下一篇: 如何更换QQ聊天背景
-
 揭秘金字塔模型的神奇公式资讯攻略02-15
揭秘金字塔模型的神奇公式资讯攻略02-15 -
 Excel求和技巧大揭秘!轻松掌握求和公式资讯攻略11-01
Excel求和技巧大揭秘!轻松掌握求和公式资讯攻略11-01 -
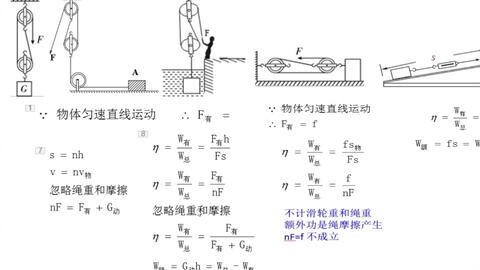 机械效率计算公式推导资讯攻略11-01
机械效率计算公式推导资讯攻略11-01 -
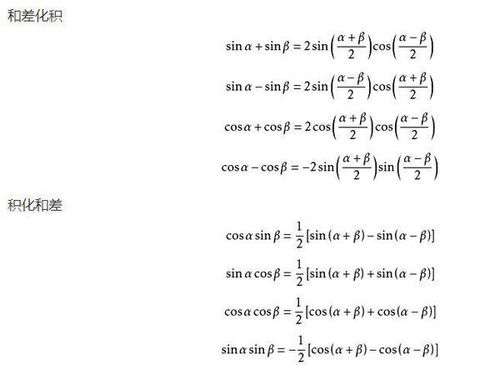 掌握常见三角函数积分公式:推导技巧与全面总结资讯攻略11-19
掌握常见三角函数积分公式:推导技巧与全面总结资讯攻略11-19 -
 等差数列前n项和该怎么求?资讯攻略11-13
等差数列前n项和该怎么求?资讯攻略11-13 -
 你了解错位相减法的奥秘吗?轻松揭开其原理!资讯攻略02-12
你了解错位相减法的奥秘吗?轻松揭开其原理!资讯攻略02-12