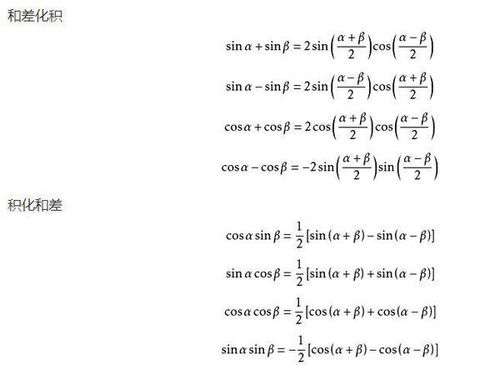机械效率计算公式推导
机械效率的推导公式是理解和评估机械性能的关键工具。机械效率是指在稳定运转时,机械的输出功(有用功)与输入功(总功)之间的百分比关系。这一概念在物理学、工程学以及日常生活中都有着广泛的应用。本文将从多个维度探讨机械效率的推导公式,包括基本公式、滑轮组的应用、斜面的效率以及实际机械中的效率分析。
机械效率的基本公式
机械效率的基本公式为:

\[ \eta = \left(\frac{W_{\text{有用}}}{W_{\text{总}}}\right) \times 100\% \]

其中,\(W_{\text{有用}}\) 代表有用功,即完成某项任务所必需的功;\(W_{\text{总}}\) 代表总功,即输入到机械中的总功。机械效率 \(\eta\) 的值在0%到100%之间,表示机械将输入功转化为有用功的能力。

滑轮组的机械效率
滑轮组是一种常见的简单机械,通过滑轮的组合可以实现省力或改变力的方向。在滑轮组中,机械效率的推导公式有几种形式,具体取决于滑轮组的配置和用途。
提升重物
在提升重物的情况下,机械效率的公式可以表示为:
\[ \eta = \frac{G_{\text{物}}}{nF} \]
其中,\(G_{\text{物}}\) 是被提升物体的重力,\(n\) 是作用在动滑轮上绳子的股数,\(F\) 是作用在绳子自由端的拉力。这个公式揭示了滑轮组省力但不省功的原理。
另一种表示方法是:
\[ \eta = \frac{G_{\text{物}}}{G_{\text{物}} + G_{\text{动}}} \]
其中,\(G_{\text{动}}\) 是动滑轮的重力。这个公式考虑了动滑轮重力对机械效率的影响。
平移重物
在平移重物的情况下,机械效率的公式可以表示为:
\[ \eta = \frac{f}{nF} \]
其中,\(f\) 是物体与水平面之间的摩擦力,\(n\) 和 \(F\) 的含义与提升重物时相同。这个公式适用于水平面上移动物体的场景。
斜面的机械效率
斜面是另一种常见的简单机械,通过增加运动路径的长度来减小所需的力。斜面的机械效率可以通过以下公式推导:
\[ \eta = \frac{G_{\text{物}}h}{FL} \]
其中,\(G_{\text{物}}\) 是被提升物体的重力,\(h\) 是斜面的高度,\(F\) 是沿斜面向上的拉力,\(L\) 是斜面的长度。这个公式表明,斜面的机械效率取决于物体的重力、斜面的几何尺寸以及所需的拉力。
实际机械中的机械效率
在实际应用中,机械效率往往受到多种因素的影响,包括摩擦、热量损失、机械部件的磨损等。因此,在实际机械中,机械效率的计算需要考虑额外功的影响。
有用功与额外功
有用功是指对人们必须要做的、有价值的功。例如,将重物提升一定高度所需做的功就是有用功。而额外功是指不必要但仍然必须做的功,例如克服摩擦力和动滑轮重力所做的功。
总功等于有用功与额外功之和:
\[ W_{\text{总}} = W_{\text{有用}} + W_{\text{额外}} \]
在实际机械中,由于额外功的存在,机械效率往往低于100%。
机械效率的推导
以滑轮组为例,假设用滑轮组提升重物,重物上升高度为 \(h\),拉力为 \(F\),绳子移动距离为 \(L\),绳子段数为 \(n\)。总功 \(W_{\text{总}}\) 可以表示为 \(FL\),有用功 \(W_{\text{有用}}\) 可以表示为 \(G_{\text{物}}h\)。因此,机械效率 \(\eta\) 可以推导为:
\[ \eta = \left(\frac{W_{\text{有用}}}{W_{\text{总}}}\right) \times 100\% = \left(\frac{G_{\text{物}}h}{FL}\right) \times 100\% \]
对于斜面,假设斜面长度为 \(L\),高度为 \(h\),物体重力为 \(G_{\text{物}}\),沿斜面的拉力为 \(F\),摩擦力为 \(f\)。总功 \(W_{\text{总}}\) 可以表示为 \(FL\),有用功 \(W_{\text{有用}}\) 可以表示为 \(G_{\text{物}}h\),额外功 \(W_{\text{额外}}\) 可以表示为 \(fL\)。因此,机械效率 \(\eta\) 可以推导为:
\[ \eta =
- 上一篇: 如何轻松设置Word文档的分栏分割线
- 下一篇: 酱香四溢的飞蟹炒制秘籍
-
 正方形对角线计算公式的推导方法资讯攻略11-28
正方形对角线计算公式的推导方法资讯攻略11-28 -
 掌握常见三角函数积分公式:推导技巧与全面总结资讯攻略11-19
掌握常见三角函数积分公式:推导技巧与全面总结资讯攻略11-19 -
 半圆面积的计算公式是什么?资讯攻略10-29
半圆面积的计算公式是什么?资讯攻略10-29 -
 揭秘长方体周长计算的奥秘公式资讯攻略11-14
揭秘长方体周长计算的奥秘公式资讯攻略11-14 -
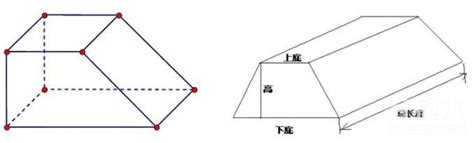 揭秘梯形体积计算:轻松掌握公式秘籍资讯攻略10-30
揭秘梯形体积计算:轻松掌握公式秘籍资讯攻略10-30 -
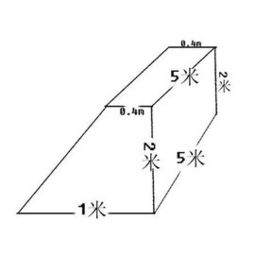 揭秘梯形体积计算的神秘公式!资讯攻略11-10
揭秘梯形体积计算的神秘公式!资讯攻略11-10