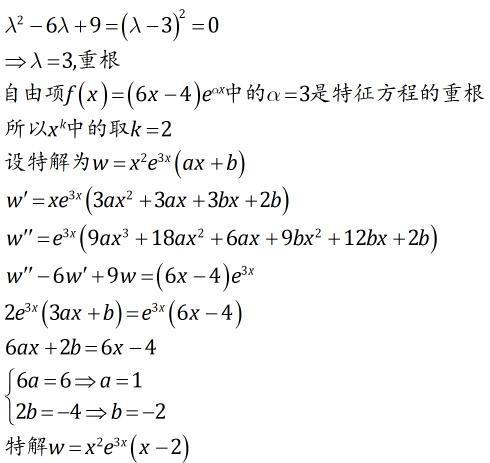揭秘:波动方程的三大经典表达形式
波动方程,这一在物理学中占据重要地位的偏微分方程,描述了自然界中各种波动现象,如声波、光波和水波等。它不仅在声学、电磁学和流体力学等领域有着广泛应用,还是理解波动现象和传播规律的基础。波动方程有多种表达形式,这些形式从不同的角度揭示了波动的本质特性。本文将详细介绍波动方程的三种主要表达式:正弦形式、余弦形式以及复数形式,帮助您更好地理解和应用这一重要的物理概念。

正弦形式的波动方程
正弦形式的波动方程通常表达为:Y = A sin(ωt - kz + φ)。

在这个表达式中:

Y 代表波动量,可以是位移、压强、电场强度等物理量。

A 是振幅,表示波动的最大幅度。
ω 是角频率,与波动的频率f相关,具体为ω = 2πf。
t 是时间,表示波动随时间的变化。
k 是波数,与波长λ相关,具体为k = 2π/λ。
z 代表位移,通常指波动在空间中传播的位置。
φ 是初相位,表示波动在初始时刻的相位。
正弦形式的波动方程适用于描述波动在空间中传播的情况,尤其是当波动呈现正弦波形时。例如,声波在空气中的传播就可以用这种形式的波动方程来描述。通过分析这个方程,我们可以了解波动的传播速度、波长、频率等基本特性。
余弦形式的波动方程
余弦形式的波动方程则表达为:Y = A cos[ω(t - kz) + φ]。
这个表达式与正弦形式非常相似,只是在三角函数上有所不同。余弦形式的波动方程同样描述了波动在空间中的传播特性,适用于多种波动现象。
在实际应用中,正弦和余弦形式的波动方程往往是等价的,因为正弦和余弦函数具有相同的周期性和振幅,只是相位上相差π/2。因此,在选择使用哪种形式的波动方程时,主要取决于问题的具体背景和便利性。
复数形式的波动方程
复数形式的波动方程则更加抽象和通用,通常表达为:Y = A e^(i(kx - ωt + φ))。
在这个表达式中:
Y、A、k、ω、t、z 和 φ 的含义与前面相同。
i 是虚数单位,满足i^2 = -1。
复数形式的波动方程利用了复数的性质,将波动量表示为一个复数函数的实部或虚部。这种形式在解析信号和频域分析中非常有用,因为它允许我们将波动现象分解为不同频率和相位的成分,从而更容易进行数学处理和物理分析。
复数形式的波动方程还揭示了波动现象中的许多重要性质,如波的传播速度、波的叠加原理以及波的干涉和衍射现象等。通过分析这个方程,我们可以更深入地理解波动现象的本质和规律。
波动方程的应用
波动方程在物理学和工程学等多个领域有着广泛的应用。以下是几个典型的例子:
1. 声学:在声学中,波动方程用于描述声波在空气中的传播特性。通过分析声波的传播规律,我们可以设计更有效的声音传播和接收设备,如扬声器、麦克风和耳机等。此外,波动方程还可以用于研究声音在固体和液体中的传播特性,为材料科学和地震学等领域提供理论基础。
2. 电磁学:在电磁学中,波动方程描述了电磁波在空间中的传播特性。电磁波包括可见光、无线电波、微波等,它们在通信、广播、雷达和医疗等领域有着广泛的应用。通过分析电磁波的传播规律,我们可以设计更高效的天线、传输线和接收器等设备,提高通信质量和效率。
3. 流体力学:在流体力学中,波动方程用于描述水波、海浪等流体波动现象。通过分析这些波动现象的传播特性,我们可以预测和防止海洋灾害,如海啸和风暴潮等。此外,波动方程还可以用于研究流体在管道和容器中的流动特性,为水利工程和化工等领域提供理论基础。
4. 地震学:在地震学中,波动方程用于描述地震波在地球内部的传播特性。通过分析地震波的传播规律,我们可以了解地球的内部结构和组成,为地质勘探和地震预警等领域提供重要信息。
波动方程的求解
波动方程的求解是一个复杂而有趣的问题。在实际应用中,我们通常采用数值方法或近似方法来求解波动方程,如有限差分法、有限元法和谱方法等。这些方法通过将波动方程离散化或近似化,转化为一系列代数方程或微分方程进行求解。
在求解波动方程时,我们还需要考虑边界条件和初始条件的影响。边界条件描述了波动在介质边界上的行为,如反射、折射和吸收等。初始条件则描述了波动在初始时刻的状态和分布。这些条件对于确定波动
- 上一篇: 《《年轻的母亲》第一部中岳母角色由谁扮演》
- 下一篇: 解析:AnyWay的含义是什么
-
 揭秘:制取氧气的三大神奇方程式资讯攻略11-14
揭秘:制取氧气的三大神奇方程式资讯攻略11-14 -
 如何求解分数方程式资讯攻略11-11
如何求解分数方程式资讯攻略11-11 -
 如何在GeoGebra图形计算器中绘制爱心资讯攻略10-28
如何在GeoGebra图形计算器中绘制爱心资讯攻略10-28 -
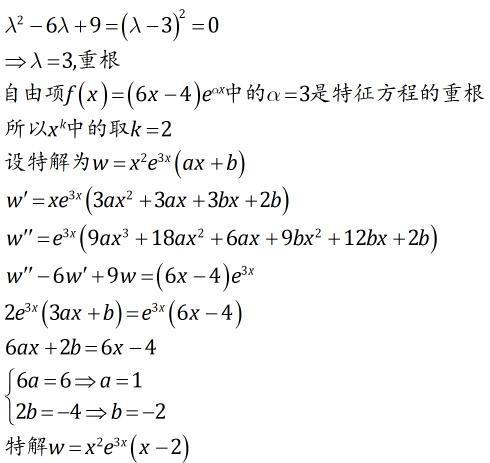 常微分方程的通解表达式是什么资讯攻略12-06
常微分方程的通解表达式是什么资讯攻略12-06 -
 揭秘:二阶微分方程的3种必备通解公式资讯攻略11-22
揭秘:二阶微分方程的3种必备通解公式资讯攻略11-22 -
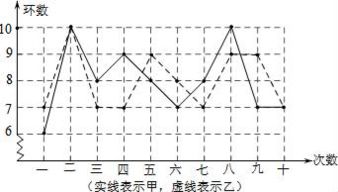 揭秘数据世界的三大秘密武器:众数、中位数与方差资讯攻略01-15
揭秘数据世界的三大秘密武器:众数、中位数与方差资讯攻略01-15