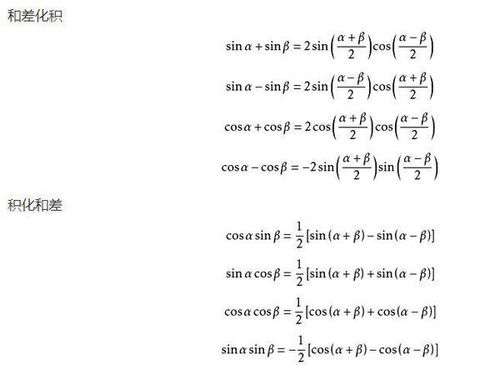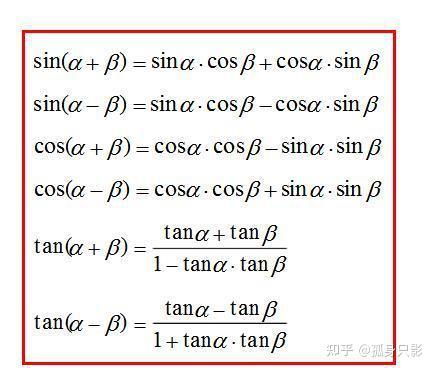三角函数常见公式都有哪些?
在数学的浩瀚宇宙中,三角函数犹如璀璨的星辰,点亮了解决几何与代数问题的道路。它们不仅是连接平面几何与立体几何的桥梁,更是解决物理、工程乃至天文学问题的重要工具。掌握三角函数的常见公式,就像手握一把万能钥匙,能轻松开启数学殿堂的大门。今天,就让我们一起踏上这场探索三角函数常见公式的奇妙之旅吧!
初探三角函数
三角函数,简单来说,是描述直角三角形中边长与角度之间关系的函数。常见的三角函数有正弦(sin)、余弦(cos)、正切(tan)、余切(cot)、正割(sec)和余割(csc)。其中,sin、cos、tan是基础中的基础,它们与直角三角形的对边、邻边和斜边紧密相连。
想象一下,你站在一个直角三角形的一个锐角顶点上,面朝直角边,背后是斜边,那么:
正弦(sin)就是你面前的对边长度除以斜边长度。
余弦(cos)则是你背后的邻边长度除以斜边长度。
正切(tan)则是你对边的长度除以邻边的长度。
三角函数的周期性与奇偶性
在深入探索公式之前,我们先来了解三角函数的两个重要性质:周期性和奇偶性。
周期性:三角函数是周期函数,意味着它们的值会在一定区间内重复。例如,正弦和余弦函数的周期为2π,意味着sin(θ) = sin(θ + 2πn),其中n是任意整数。
奇偶性:正弦和正切函数是奇函数,即sin(-θ) = -sin(θ),tan(-θ) = -tan(θ);而余弦、余切、正割和余割函数则是偶函数,即cos(-θ) = cos(θ),cot(-θ) = cot(θ)等。
常见三角函数公式大赏
基础公式
1. 互余角公式:sin(90° - α) = cos(α),cos(90° - α) = sin(α),tan(90° - α) = 1/tan(α)。这些公式揭示了正弦与余弦、正切与余切之间的互补关系。
2. 同角关系:sin²(α) + cos²(α) = 1,1 + tan²(α) = sec²(α),1 + cot²(α) = csc²(α)。这些公式是三角函数之间最基本的关系,也是推导其他公式的基础。
和差公式
1. 正弦和差公式:sin(α ± β) = sin(α)cos(β) ± cos(α)sin(β)。这个公式让我们能够计算两个角的和或差的正弦值,是三角函数运算中的“瑞士军刀”。
2. 余弦和差公式:cos(α ± β) = cos(α)cos(β) ∓ sin(α)sin(β)。注意这里的符号变化,与正弦和差公式形成对比。
3. 正切和差公式:tan(α ± β) = [tan(α) ± tan(β)] / [1 ∓ tan(α)tan(β)]。这个公式稍显复杂,但掌握后能帮助我们解决许多复杂的三角函数问题。
倍角公式
1. 正弦倍角公式:sin(2α) = 2sin(α)cos(α)。这个公式让我们能够轻松计算二倍角的正弦值。
2. 余弦倍角公式:cos(2α) = cos²(α) - sin²(α) = 2cos²(α) - 1 = 1 - 2sin²(α)。这三个等价形式展示了余弦倍角的多种表达方式,便于在不同情境下灵活应用。
3. 正切倍角公式:tan(2α) = [2tan(α)] / [1 - tan²(α)]。这个公式虽然看起来复杂,但掌握后能够大大提高解题效率。
半角公式
1. 正弦半角公式:sin(α/2) = ±√[(1 - cos(α)) / 2]。注意这里的正负号取决于α/2所在的象限。
2. 余弦半角公式:cos(α/2) = ±√[(1 + cos(α)) / 2]。同样,正负号的选择取决于α/2的象限。
3. 正切半角公式:tan(α/2) = ±√[(1 - cos(α)) / (1 + cos(α))] = (1 - cos(α)) / sin(α) = sin(α) / (1 + cos(α))。这个公式有多种等价形式,选择哪种取决于已知条件和计算便捷性。
积化和差公式与和差化积公式
1. 积化和差公式:这些公式允许我们将两个三角函数的乘积转化为和或差的形式,如sin(α)cos(β) = [sin(α + β) + sin(α - β)] / 2等。这类公式在简化表达式和求解方程时非常有用。
2. 和差化积公式:与积化和差公式相反,这些公式将和或差转化为乘积形式,如sin(α + β) + sin(α - β) = 2sin(α)cos(β)等。在解决某些特定类型的问题时,这些公式能带来意想不到的便利。
三角函数公式的应用
掌握这些公式后,我们可以解决从简单的几何问题到复杂的物理和工程问题。例如,在信号处理中,正弦和余弦函数用于描述波形;在力学中,正切函数用于计算斜面的坡度;在天文学中,三角函数则用于计算天体之间的角度关系。
结语
三角函数公式虽多,但只要理解其背后的几何意义,掌握推导方法,就能游刃有余地应用它们。就像掌握一门语言需要不断练习一样,学习三角函数也需要通过大量的练习来巩固知识、提升技能。希望这篇文章能激发你对三角函数的兴趣,引领你在数学的海洋中乘风破浪,探索未知。记住,每一个公式都是前人智慧的结晶,每一次应用都是对知识的最好致敬。让我们携手前行,在数学的奇妙世界中共同成长吧!
- 上一篇: 揭秘上海法租界:历史遗迹与现代地标的边界探索
- 下一篇: 如何正确张贴春联的上下联
-
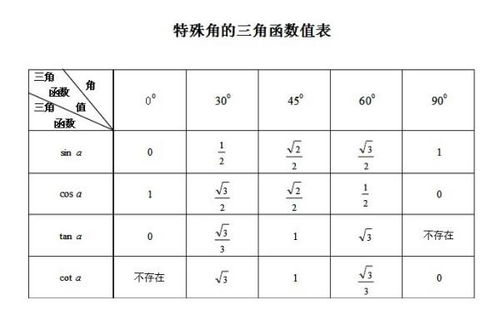 三角函数值表有哪些常见内容?资讯攻略11-02
三角函数值表有哪些常见内容?资讯攻略11-02 -
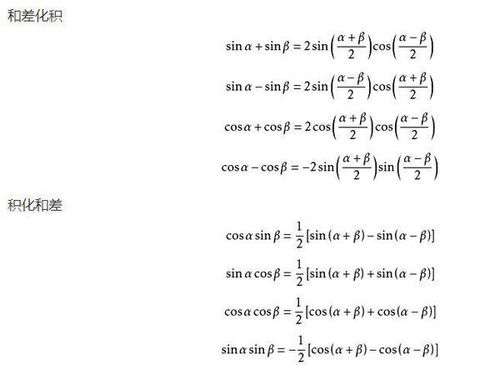 掌握常见三角函数积分公式:推导技巧与全面总结资讯攻略11-19
掌握常见三角函数积分公式:推导技巧与全面总结资讯攻略11-19 -
 三角形边长关系公式详解资讯攻略11-20
三角形边长关系公式详解资讯攻略11-20 -
 Excel中如何进行减法运算的函数公式资讯攻略11-19
Excel中如何进行减法运算的函数公式资讯攻略11-19 -
 Excel中如何进行数值相减的函数公式是什么?资讯攻略12-02
Excel中如何进行数值相减的函数公式是什么?资讯攻略12-02 -
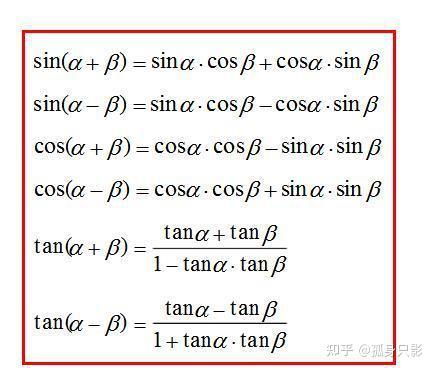 掌握三角函数公式,轻松解题无压力!资讯攻略11-28
掌握三角函数公式,轻松解题无压力!资讯攻略11-28