三角形边长关系公式详解

三角形边长公式是几何学中的一个基础而重要的概念，它不仅在解决三角形相关问题中起到关键作用，还是进一步学习更复杂几何知识的基础。在探讨三角形边长公式时，我们可以从多个维度入手，包括定义与基本概念、常见类型三角形的边长关系、海伦公式及其应用、余弦定理及其应用，以及三角形边长公式在实际问题中的应用。

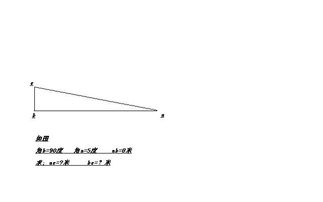
三角形是几何学中最基本的图形之一，它由三条边和三个顶点组成。在讨论三角形的边长公式时，我们首先需要明确一些基本概念。三角形的边长指的是连接三角形三个顶点的三条线段的长度，分别记作a、b、c。根据三角形的性质，任意两边之和大于第三边，任意两边之差小于第三边，这是三角形边长关系的基本定理，也是判断三条线段能否构成三角形的重要依据。

在探讨三角形边长公式时，不同类型的三角形有其特定的边长关系。首先，等边三角形的三条边长相等，即a=b=c。这种三角形具有最高的对称性，其边长关系最为简单。其次，等腰三角形有两条边长相等，记作a=b或b=c或a=c（取决于哪两条边相等）。在等腰三角形中，除了两条相等的边外，还有一条底边和两个相等的底角。最后，对于一般的三角形，即三边长度都不相等的三角形，我们需要借助更复杂的公式来计算其边长关系。

海伦公式是解决三角形边长问题的一个重要工具。海伦公式，又称赫伦公式，是一种利用三角形的三边长度来计算其面积的方法。其表达式为：面积S=√(p(p-a)(p-b)(p-c))，其中p为三角形的半周长，即p=(a+b+c)/2。虽然海伦公式本身不是直接用来计算三角形边长的，但通过它可以推导出一些与边长相关的结论。例如，在已知三角形的面积和两条边长的情况下，可以利用海伦公式求出第三条边的长度。

余弦定理是另一个解决三角形边长问题的关键公式。余弦定理表述为：对于任意三角形，其任意一边的平方等于其他两边的平方和减去这两边与其夹角的余弦的积的两倍。即c²=a²+b²-2abcosC（或a²=b²+c²-2bccosA，b²=a²+c²-2accosB）。余弦定理在三角形边长计算中非常有用，特别是在已知两边长度和夹角的情况下。通过余弦定理，我们可以直接求出第三边的长度，或者解决一些与三角形边长相关的问题，如判断三角形的形状等。

在实际应用中，三角形边长公式具有广泛的用途。在建筑设计领域，工程师们需要利用三角形边长公式来计算建筑物的尺寸和角度，以确保结构的稳定性和美观性。在航空航天领域，科学家和工程师们需要利用这些公式来计算飞行器的轨迹和姿态，以确保其能够安全、准确地到达目的地。此外，在地理信息系统（GIS）中，三角形边长公式也被用来计算地理空间中的距离和角度，以支持地图制作和导航等功能。

除了上述领域外，三角形边长公式还在物理学、天文学、机械工程等领域发挥着重要作用。在物理学中，三角形边长公式被用来计算物体的运动轨迹和速度等参数；在天文学中，科学家们利用这些公式来计算星体的位置和距离；在机械工程中，工程师们需要利用这些公式来设计机器零件的尺寸和形状等。

在解决三角形边长问题时，我们还需要注意一些特殊情况。例如，当三角形为直角三角形时，我们可以利用勾股定理（a²+b²=c²）来计算其边长关系。勾股定理是直角三角形边长关系的基本定理，也是解决直角三角形问题的关键工具。此外，在求解三角形边长问题时，我们还需要注意单位换算和精度控制等问题，以确保计算结果的准确性和可靠性。

此外，三角形边长公式在解题过程中还可以与其他几何知识和方法相结合，形成更强大的解题能力。例如，我们可以将三角形边长公式与向量方法相结合，利用向量的性质和运算来求解三角形边长问题。这种方法在处理复杂问题时特别有效，能够简化计算过程并提高解题效率。

在学习三角形边长公式时，我们还需要注意培养自己的几何直觉和空间想象能力。通过大量的练习和实践，我们可以逐渐掌握这些公式的应用方法和技巧，提高自己的解题能力和几何素养。同时，我们还可以利用现代化的计算工具和技术来辅助学习和解题，如计算器、计算机程序等。这些工具能够帮助我们更快速、准确地计算三角形的边长和其他相关参数。

总之，三角形边长公式是几何学中的一个重要概念，它在解决三角形相关问题中发挥着关键作用。通过学习和掌握这些公式，我们可以更好地理解和应用几何学知识，提高自己的解题能力和几何素养。同时，这些公式还具有广泛的应用价值，能够支持我们在多个领域中进行科学研究和工程实践。因此，我们应该重视三角形边长公式的学习和应用，不断探索和实践其在实际问题中的解决方案和方法。