掌握求解三角函数解析式的多种高效方法

求解三角函数的解析式的几种方法

三角函数解析式是三角函数的核心内容之一，在三角函数图象与性质、三角函数的应用等问题的解决中，起着举足轻重的作用。求三角函数解析式问题，综合性强，方法灵活，现就求三角函数解析式的几种常见方法举例分析。

一、已知函数类型，求参数

例1：已知函数 f(x)=Asin(ωx+φ)（A>0，ω>0，|φ|<π）的最小正周期为 π，且图象上有一个最低点 M(2π/3，-2)，求 f(x) 的解析式。

解：由最低点 M(2π/3，-2) 得 A=2。

由最小正周期 T=π 得 ω=2π/T=2。

于是可设 f(x)=2sin(2x+φ)，因为 f(2π/3)=2sin(2×2π/3+φ)=-2，

所以 sin(4π/3+φ)=-1，

所以 4π/3+φ=2kπ-π/2，k∈Z，

所以 φ=2kπ-11π/6，k∈Z，

又 |φ|<π，所以 φ=π/6，

所以 f(x)=2sin(2x+π/6)。

二、已知部分图象，求解析式

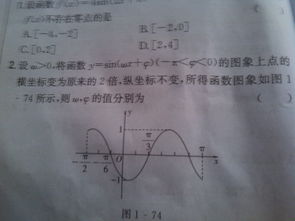
例2：已知函数 y=Asin(ωx+φ)（A>0，ω>0，|φ|<π）的图象上一个最高点为 P(2，2)，由这个最高点到相邻最低点间的曲线与 x 轴交于点 Q(6，0)，求这个函数的解析式。

解：由最高点 P(2，2) 得 A=2。

由最高点到相邻最低点间的曲线与 x 轴交于点 Q(6，0)，得 1/4×2π/ω=6-2，解得 ω=1/4×(2π/4)=π/8。

于是可设 y=2sin(π/8x+φ)，

因为函数图象过点 Q(6，0)，所以 2sin(6×π/8+φ)=0，

所以 6×π/8+φ=kπ，k∈Z，

所以 φ=kπ-3π/4，k∈Z，

又 |φ|<π，所以 φ=π/4，

所以所求函数解析式为 y=2sin(π/8x+π/4)。

三、已知函数图象的变换关系，求解析式

例3：已知函数 y=sinx 的图象经过平移或伸缩变换得到 y=f(x) 的图象，且 f(0)=0，f(π/2)=1，f(π)=-1，求 f(x) 的解析式。

解：由题意设 f(x)=Asin(ωx+φ)（A>0，ω>0，|φ|<π/2）。

因为 f(0)=0，所以 φ=kπ，k∈Z，

又因为 |φ|<π/2，所以 φ=0。

所以 f(x)=Asinωx。

因为 f(π/2)=1，所以 A=1 或 A=-1（舍去）。

所以 f(x)=sinωx。

因为 f(π)=-1，所以 sinωπ=-1，

所以 ωπ=2kπ-π/2，k∈Z，

所以 ω=2k-1/2，k∈Z。

又因为 ω>0，所以 ω 的最小值为 1/2。

所以 f(x)=sin(1/2x)。

四、利用两角和与差的正弦、余弦公式求解析式

例4：已知 f(x)=2cos²x+2√3sinxcosx-1。

（1）化简 f(x) 的解析式，并求函数 f(x) 的最小正周期；

（2）求函数 f(x) 在区间 [0，π/2] 上的最大值和最小值。

解：（1）f(x)=2cos²x+2√3sinxcosx-1=cos2x+√3sin2x=2sin(2x+π/6)。

所以函数 f(x) 的最小正周期为 T=2π/2=π。

（2）因为 x∈[0，π/2]，所以 2x+π/6∈[π/6，7π/6]。

所以当 2x+π/6=π/2 时，f(x) 取得最大值 2；

当 2x+π/6=7π/6 时，f(x) 取得最小值 -1。

五、利用辅助角公式求解析式

例5：已知函数 f(x)=2√3sinxcosx-2cos²x+1。

（1）求函数 f(x) 的最小正周期及单调递增区间；

（2）求函数 f(x) 在区间 [-π/6，π/3] 上的最大值和最小值。

解：（1）f(x)=2√3sinxcosx-2cos²x+1=√3sin2x-cos2x=2sin(2x-π/6)。

所以函数 f(x) 的最小正周期为 T=2π/2=π。

由 2kπ-π/2≤2x-π/6≤2kπ+π/2，k∈Z，

得 kπ-π/6≤x≤kπ+π/3，k∈Z，

所以函数 f(x) 的单调递增区间为 [kπ-π/6，kπ+π/3]，k∈Z。

（2）因为 x∈[-π/6，π/3]，所以 2x-π/6∈[-π/2，π/2]。

所以当 2x-π/6=π/2 时，f(x) 取得最大值 2；

当 2x-π/6=-π/2 时，f(x) 取得最小值 -2。

六、利用方程组法求解析式

例6：已知函数 f(x)=Acos(ωx+φ)+B（A>0，ω>0，|φ|<π）的最大值为 2，最小值为 -4，周期为 π，求 f(x) 的解析式。

解：由题意得 A+B=2，-A+B=-4，

解得 A=3，B=-1。

所以 f(x)=3cos(ωx+φ)-1。

又因为 T=π，所以 ω=2π/T=2。

所以 f(x)=3cos(2x+φ)-1。

因为 f(x) 的图象经过点 (0，-1)，所以 3cosφ-1=-1，

所以 cosφ=0，

所以 φ=kπ+π/2，k∈Z，

又 |φ|<π，所以 φ=π/2。

所以 f(x)=3cos(2x+π/2)-1=-3sin2x-1。

求三角函数解析式问题的常见类型主要有以上六种，在解题过程中，要注意结合题目所给的条件，灵活选择恰当的方法，以达到迅速解题的目的。