揭秘:交集与并集的神秘符号大起底!
在数学的世界里,我们经常会遇到各种各样的符号,它们就像是数学语言的字母和单词,帮助我们表达复杂的逻辑和关系。其中,交集和并集是两个非常重要的概念,它们描述了两个集合之间可能存在的两种基本关系。那么,交集并集符号是什么呢?让我们一起揭开它们的神秘面纱。
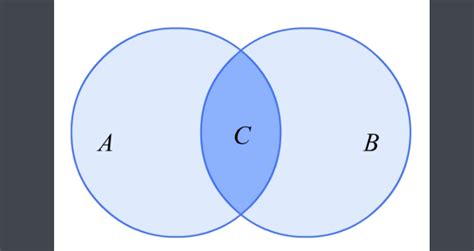
交集符号:∩
首先,我们来聊聊交集。想象一下,你有两个装满水果的篮子,一个篮子里有苹果和香蕉,另一个篮子里有香蕉和橙子。现在,如果你想知道这两个篮子里共同拥有的水果是什么,你会怎么做?很简单,你只需看看哪些水果在两个篮子里都出现了。这个“共同出现”的过程,在数学上就被称为“交集”。

交集符号是一个大大的倒写的“U”,中间有一个小圆点或者干脆就是一个实心的小圆圈,写作“∩”。当我们说A和B的交集时,我们是在寻找同时属于A和B的元素组成的集合。用符号表示就是:A ∩ B。
比如,如果我们有两个集合:
A = {1, 2, 3, 4}
B = {3, 4, 5, 6}
那么,A和B的交集就是:
A ∩ B = {3, 4}
这意味着,数字3和4同时出现在集合A和集合B中。
并集符号:∪
接下来,我们谈谈并集。还是那两个装满水果的篮子,但这次我们的目标是找出两个篮子里所有的水果,不管它们是否重复。换句话说,我们想要的是两个篮子里水果的总和,但每个水果只计算一次。这个过程,在数学上被称为“并集”。
并集符号是一个大大的正写的“U”,中间没有小圆点,写作“∪”。当我们说A和B的并集时,我们是在寻找属于A或B(或两者都属于)的元素组成的集合。用符号表示就是:A ∪ B。
继续用上面的例子:
A = {1, 2, 3, 4}
B = {3, 4, 5, 6}
那么,A和B的并集就是:
A ∪ B = {1, 2, 3, 4, 5, 6}
这意味着,我们列出了集合A和集合B中所有的数字,但每个数字只出现了一次。
交集与并集的应用
交集和并集的概念不仅限于简单的数字集合,它们广泛应用于数学、计算机科学、统计学、物理学等众多领域。
数学:在解决集合问题时,交集和并集是基本的工具。比如,在概率论中,两个事件的交集通常表示这两个事件同时发生的概率,而并集则表示至少有一个事件发生的概率。
计算机科学:在数据库查询、信息检索等领域,交集和并集操作非常常见。比如,如果你想要找出同时满足两个搜索条件的文档,你实际上是在执行一个交集操作。而如果你想要找出满足任一搜索条件的文档,你则是在执行一个并集操作。
统计学:在数据分析中,交集和并集用于确定不同数据集之间的重叠部分和总覆盖范围。比如,在市场调研中,你可能想要知道两个不同产品线的客户群有多少是重叠的,以及它们各自的总客户群有多大。
物理学:在量子力学中,交集和并集的概念被用于描述量子态的叠加和测量结果的概率分布。
交集与并集的直观理解
为了更好地理解交集和并集,我们可以借助一些直观的图形工具,比如文氏图(Venn Diagram)。
文氏图是一种用圆形或椭圆形来表示集合的图形方法。在文氏图中,每个集合都被表示为一个独立的区域,而集合之间的关系(如交集、并集)则通过这些区域的重叠部分来展示。
交集:在文氏图中,两个集合的交集就是它们重叠的部分。这个部分同时属于两个集合。
并集:在文氏图中,两个集合的并集就是它们覆盖的总区域。这个区域包括了属于第一个集合的元素、属于第二个集合的元素,以及同时属于两个集合的元素(但每个元素只计算一次)。
通过文氏图,我们可以直观地看到交集和并集是如何工作的,这对于理解这些概念非常有帮助。
交集与并集的运算规则
在进行交集和并集运算时,有一些基本的规则需要遵循:
交集运算规则:
A ∩ B = B ∩ A(交集满足交换律)
(A ∩ B) ∩ C = A ∩ (B ∩ C)(交集满足结合律)
A ∩ A = A(任何集合与自身的交集就是该集合本身)
A ∩ ∅ = ∅(任何集合与空集的交集是空集)
并集运算规则:
A ∪ B = B ∪ A(并集满足交换律)
(A ∪ B) ∪ C = A ∪ (B ∪ C)(并集满足结合律)
A ∪ A = A(任何集合与自身的并集就是该集合本身)
A ∪ ∅ = A(任何集合与空集的并集是该集合本身)
A ∪ U = U(任何集合与全集的并集是全集)
这些规则帮助我们在进行交集和并集运算时保持一致性,确保我们的结果是正确的。
结语
通过这篇文章,我们详细介绍了交集和并集的概念、符号、应用以及运算规则。交集和并集是数学中非常重要的基础概念,它们不仅在数学内部有着广泛的应用,还跨越到其他学科领域,成为我们理解和解决复杂问题的重要工具。希望这篇文章能够帮助你更好地理解交集和并集,让你在数学学习的道路上更加得心应手。
- 上一篇: 如何让煎出的牛排又嫩又美味?
- 下一篇: OPPO手机如何开启地震预警功能,关键时刻守护安全
-
 揭秘交集并集符号:一看就懂的解释!资讯攻略12-01
揭秘交集并集符号:一看就懂的解释!资讯攻略12-01 -
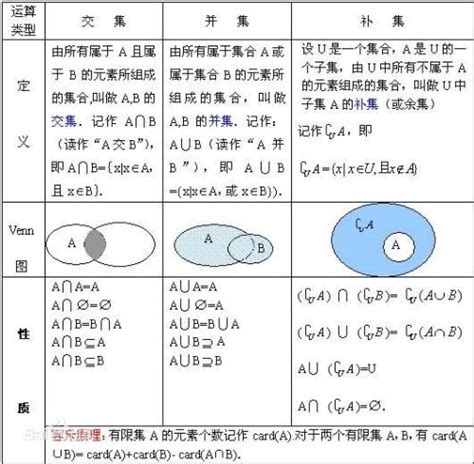 轻松区分交集与并集,一文读懂!资讯攻略12-01
轻松区分交集与并集,一文读懂!资讯攻略12-01 -
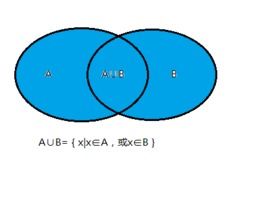 探索集合世界:揭秘交集、并集与补集的奥秘资讯攻略12-01
探索集合世界:揭秘交集、并集与补集的奥秘资讯攻略12-01 -
 揭秘!发光二极管电路图中的神秘符号大起底资讯攻略11-04
揭秘!发光二极管电路图中的神秘符号大起底资讯攻略11-04 -
 揭秘!FANK:一款令人瞩目的神秘车型大起底资讯攻略11-21
揭秘!FANK:一款令人瞩目的神秘车型大起底资讯攻略11-21 -
 揭秘!0190852213号码归属地大起底资讯攻略03-13
揭秘!0190852213号码归属地大起底资讯攻略03-13












