轻松区分交集与并集，一文读懂！

在数学的广阔领域中，集合论占据着举足轻重的地位。作为集合论中的两个基本概念，交集和并集不仅在日常的数学学习中频繁出现，更在解决实际问题时发挥着重要作用。然而，对于初学者而言，如何准确区分交集和并集，往往是一个需要细致琢磨的过程。本文旨在通过详细阐述交集和并集的定义、性质、应用场景以及它们之间的区别，帮助读者更好地理解和掌握这两个概念。

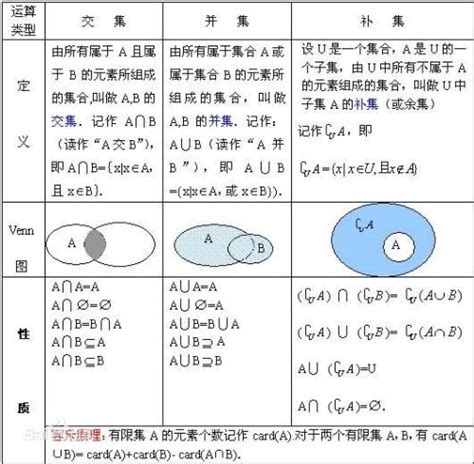
首先，我们来看交集。交集，顾名思义，是指两个或多个集合中共同的元素所组成的集合。换句话说，如果某个元素同时属于两个或多个给定的集合，那么这个元素就属于这些集合的交集。例如，设集合A为{1, 2, 3, 4}，集合B为{3, 4, 5, 6}，那么集合A与集合B的交集，记作A∩B，就是{3, 4}。在这个例子中，3和4是集合A和集合B共有的元素，因此它们构成了两个集合的交集。

交集具有一些重要的性质。首先，交集运算满足交换律和结合律，即A∩B=B∩A，以及(A∩B)∩C=A∩(B∩C)。其次，任何集合与空集的交集都是空集，即A∩∅=∅。此外，任何集合与其自身的交集就是该集合本身，即A∩A=A。这些性质使得交集运算在数学推理和证明中具有重要的应用价值。

在实际应用中，交集的概念被广泛用于数据筛选、条件筛选等场景。例如，在数据分析中，我们可能需要找出同时满足多个条件的记录。这些记录就可以看作是满足条件的各个集合的交集。通过计算交集，我们可以快速定位到满足所有条件的记录，从而进行进一步的分析和处理。

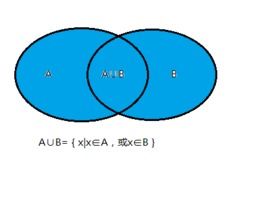
接下来，我们探讨并集。与交集不同，并集是指两个或多个集合中所有元素（包括重复元素只计算一次）所组成的集合。换句话说，如果某个元素属于两个或多个给定的集合中的任何一个，那么这个元素就属于这些集合的并集。以集合A={1, 2, 3, 4}和集合B={3, 4, 5, 6}为例，集合A与集合B的并集，记作A∪B，就是{1, 2, 3, 4, 5, 6}。在这个例子中，1、2、5和6分别只属于集合A或集合B，而3和4同时属于两个集合，但在并集中只计算一次。

并集同样具有一些重要的性质。首先，并集运算也满足交换律和结合律，即A∪B=B∪A，以及(A∪B)∪C=A∪(B∪C)。其次，任何集合与空集的并集都是该集合本身，即A∪∅=A。此外，任何集合与其自身的并集仍然是该集合本身，即A∪A=A。这些性质使得并集运算在数学和实际应用中同样具有广泛的应用价值。

在实际应用中，并集的概念常用于数据合并、条件合并等场景。例如，在数据挖掘中，我们可能需要将来自不同数据源的数据进行合并。这些数据可以看作是不同集合的元素，通过计算并集，我们可以得到包含所有元素的新数据集，从而进行更全面的分析和挖掘。

在区分交集和并集时，我们需要注意以下几点：首先，交集关注的是两个或多个集合中共有的元素，而并集则关注的是两个或多个集合中所有的元素（包括重复元素只计算一次）。其次，从符号表示上看，交集使用“∩”表示，而并集使用“∪”表示。最后，从运算结果上看，交集的结果通常包含的元素数量较少（甚至可能为空集），而并集的结果则包含的元素数量较多（甚至可能包含所有可能的元素）。

为了更好地理解交集和并集的区别，我们可以通过一些具体的例子进行说明。例如，假设我们有两个集合：集合C为{苹果, 香蕉, 橙子}，集合D为{香蕉, 葡萄, 橙子}。那么，集合C与集合D的交集C∩D就是{香蕉, 橙子}，因为它们是两个集合中共有的元素。而集合C与集合D的并集C∪D则是{苹果, 香蕉, 橙子, 葡萄}，因为它们包含了两个集合中所有的元素（重复元素只计算一次）。

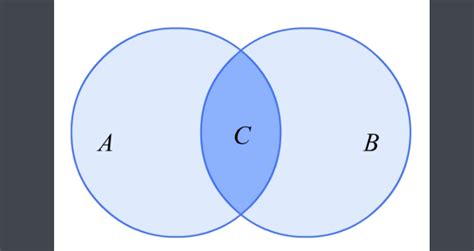
此外，我们还可以利用文氏图来直观地表示交集和并集的关系。在文氏图中，每个集合通常用一个圆圈来表示，圆圈内的元素属于该集合。交集可以看作是两个或多个圆圈重叠的部分，而并集则可以看作是两个或多个圆圈及其重叠部分的总和。通过文氏图，我们可以更加直观地理解交集和并集的概念及其区别。

综上所述，交集和并集作为集合论中的两个基本概念，在数学和实际应用中都具有广泛的应用价值。通过准确理解交集和并集的定义、性质以及它们之间的区别，我们可以更好地运用这些概念来解决实际问题。同时，我们也可以利用文氏图等辅助工具来直观地表示和理解交集和并集的关系，从而加深对这两个概念的认识和掌握。