探索集合世界：揭秘交集、并集与补集的奥秘

在数学领域中，集合论是一个重要的分支，它不仅为数学研究提供了坚实的基础，也在计算机科学、统计学等多个领域发挥着不可或缺的作用。在集合论的基本概念中，交集、并集和补集是三大核心概念，它们构成了理解和操作集合的基本工具。本文将详细解析这三个概念，以便读者能够清晰地掌握它们各自的定义、性质以及在实际中的应用。

首先，我们需要明确集合的定义。集合是由某些确定的对象所组成的，这些对象被称为集合的元素。集合的表示方法有多种，常用的是列举法和描述法。列举法是将集合中的元素一一列出，用逗号分隔，然后用大括号括起来。描述法则通过描述集合中元素的共同特征来定义集合。

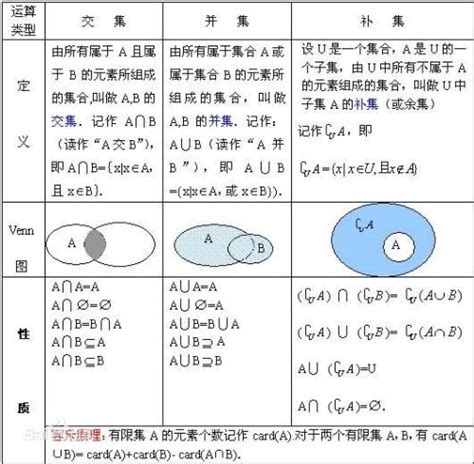
交集：

交集是指两个或多个集合中共有的元素所组成的集合。用符号表示为“∩”。例如，有两个集合A={1,2,3,4}和B={3,4,5,6}，那么它们的交集A∩B={3,4}。交集的性质包括：

1. 交换律：A∩B=B∩A，即交集的顺序不影响结果。

2. 结合律：(A∩B)∩C=A∩(B∩C)，即多个集合的交集可以分步进行。

3. 分配律：A∩(B∪C)=(A∩B)∪(A∩C)，这是交集与并集之间的一个重要关系。

4. 同一律：A∩A=A，即集合与自身的交集是其本身。

5. 零集律：A∩∅=∅，即任何集合与空集的交集是空集。

交集在实际应用中非常广泛，比如在数据分析中，我们可以使用交集来找出两个数据集中共有的元素，从而进行更深入的分析。

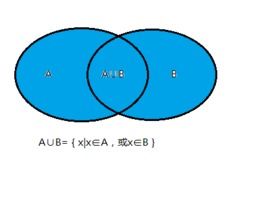
并集：

并集是指两个或多个集合中所有的元素（重复的元素只计算一次）所组成的集合。用符号表示为“∪”。例如，有两个集合A={1,2,3,4}和B={3,4,5,6}，那么它们的并集A∪B={1,2,3,4,5,6}。并集的性质包括：

1. 交换律：A∪B=B∪A，即并集的顺序不影响结果。

2. 结合律：(A∪B)∪C=A∪(B∪C)，即多个集合的并集可以分步进行。

3. 同一律：A∪A=A，即集合与自身的并集是其本身。

4. 单位元：A∪∅=A，即任何集合与空集的并集是其本身。

5. 吸收律：A∪(A∩B)=A，即集合与其与其他集合的交集的并集是其本身。

并集在实际生活中也有很多应用，比如在设计数据库时，我们可以使用并集来合并多个数据表，从而获得更全面的信息。

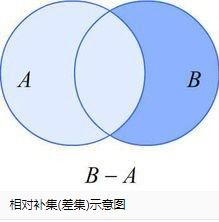
补集：

补集是指在一个全集U中，但不在某个集合A中的所有元素所组成的集合。用符号表示为“A'”或“C_U A”。例如，全集U={1,2,3,4,5,6}，集合A={1,2,3}，那么A的补集A'={4,5,6}。补集的性质包括：

1. 补集的补集：A''=A，即集合的补集的补集是其本身。

2. 补集的并集：A∪A'=U，即集合与其补集的并集是全集。

3. 补集的交集：A∩A'=∅，即集合与其补集的交集是空集。

4. 德摩根定律：(A∩B)'=A'∪B' 和 (A∪B)'=A'∩B'，这是补集与交集、并集之间的重要关系。

补集的概念在解决某些逻辑问题时非常有用，比如在逻辑推理中，我们可以使用补集来简化问题，从而更容易找到解决方案。

在实际应用中，交集、并集和补集经常需要综合运用。例如，在数据库查询中，我们可能需要先找出两个表的交集（共同的数据），然后对其中的一个表取补集（找出只在该表中存在的数据），最后再与第三个表取并集（合并数据）。这样的操作在数据处理和分析中非常常见。

此外，在集合运算中，我们还需要注意一些特殊的情况。比如，当两个集合没有交集时，它们的交集是空集；当两个集合完全相同时，它们的并集就是它们本身；当全集只有一个元素时，任何非空集合的补集都是空集，而空集的补集则是全集本身。

总的来说，交集、并集和补集是集合论中的基本概念，它们为我们提供了一种描述和操作集合的简洁而强大的工具。无论是在数学研究、计算机科学还是其他领域，这些概念都发挥着重要的作用。通过深入理解和掌握这些概念，我们可以更好地处理和分析与集合相关的问题，从而在实际应用中取得更好的效果。