如何计算相对误差?
相对误差怎么算的
相对误差是衡量测量值偏离其真实值程度的一个重要指标。在科研、工程、质量控制等多个领域中,相对误差的计算与理解都至关重要。本文将从相对误差的定义、计算公式、应用以及误差来源等多个维度详细解析相对误差的计算方法。

一、相对误差的定义
相对误差指的是测量所造成的绝对误差与被测量(约定)真值之比乘以100%所得的数值,以百分数表示。设测量结果y减去被测量约定真值t,所得的误差或绝对误差为Δ。将绝对误差Δ除以约定真值t即可求得相对误差,公式为:

\[
\text{相对误差} = \frac{\text{绝对误差}}{\text{真值}} \times 100\%
\]
其中,绝对误差是测量值与真实值之差的绝对值,它指明了误差的大小和正负方向。真值是指被测量的真实数值,但在实际操作中,真值通常是未知的或难以准确获得,常用约定真值来代替。
二、相对误差的计算公式
相对误差的计算公式可以表示为:
\[
\delta = \frac{\Delta}{L} \times 100\%
\]
其中:
\( \delta \) 是实际相对误差,一般用百分数给出。
\( \Delta \) 是绝对误差,计算公式为 \( \Delta = |y - t| \),其中 \( y \) 是测量值,\( t \) 是约定真值。
\( L \) 是真值。
例如,某甲度量长约1米的一段钢材,量得结果的绝对误差为0.01米,则相对误差为:
\[
\delta = \frac{0.01}{1} \times 100\% = 1\%
\]
三、相对误差的应用
相对误差相较于绝对误差,更能反映测量的可信程度。在实际应用中,特别是在需要比较不同测量结果的准确度时,相对误差显得尤为重要。
1. 测量结果的比较:
当测量两个或多个量时,它们的绝对误差可能相同,但相对误差却不同。例如,某乙度量长约5米的一段钢材,量得结果的绝对误差也是0.01米,则其相对误差为:
\[
\delta = \frac{0.01}{5} \times 100\% = 0.2\%
\]
虽然甲和乙的绝对误差都是0.01米,但甲的相对误差为1%,乙的相对误差为0.2%,显然乙的测量结果更为可信。
2. 实验数据的质量控制:
在科研实验中,数据的准确性至关重要。通过计算相对误差,可以评估实验数据的可靠程度,进而判断实验结果的有效性。例如,在化学分析中,不同方法的相对误差可以用来比较其准确度和适用性。
3. 仪器设备的校准:
仪器设备的准确度直接影响测量结果的可靠性。通过计算仪器测量值的相对误差,可以判断其是否符合规定标准,进而进行校准和调整,确保测量结果的准确性。
四、相对误差与绝对误差的关系
相对误差和绝对误差是两个紧密相连的概念。绝对误差是测量值与真实值之差的绝对值,它反映了测量值偏离真实值的具体大小。而相对误差是绝对误差与真值的比值,它反映了测量值偏离真实值的相对程度。
1. 绝对误差的计算:
绝对误差的计算公式为:
\[
\text{绝对误差} = |\text{测量值} - \text{真实值}|
\]
设某物理量的测量值为 \( x \),它的真值为 \( a \),则绝对误差为:
\[
\Delta = |x - a|
\]
绝对误差是一个有单位的量,与测量值和真实值的单位相同。
2. 相对误差与绝对误差的关系:
相对误差是绝对误差与真值的比值,因此它是一个无量纲的量。通过计算相对误差,可以比较不同量或不同测量结果的准确度,而不受量纲的限制。
五、误差的来源
误差的来源多种多样,主要包括以下几个方面:
1. 观测误差:
由于实际观测手段的限制,如仪器精度不足、环境条件影响等,造成的测量误差称为观测误差。这类误差通常难以完全消除,但可以通过改进观测方法和提高仪器精度来减小。
2. 截断误差:
在进行数学计算时,由于计算过程的近似性,如有限项的级数展开、有限精度的数值计算等,造成的误差称为截断误差。这类误差可以通过增加计算精度和改进计算方法来减小。
3. 舍入误差:
在计算中用有限小数代替某个已知数时,由于舍入操作造成的误差称为舍入误差。这类误差通常难以
- 上一篇: 少年崛起,铸就中国辉煌未来
- 下一篇: 微信怎么切换到夜间模式?
-
 绝对误差与相对误差的计算公式详解资讯攻略12-06
绝对误差与相对误差的计算公式详解资讯攻略12-06 -
 圆周率的计算方法详解资讯攻略11-15
圆周率的计算方法详解资讯攻略11-15 -
 CAD中计算面积的快捷键有哪些?资讯攻略11-26
CAD中计算面积的快捷键有哪些?资讯攻略11-26 -
 Excel中如何计算相对标准偏差值?资讯攻略11-22
Excel中如何计算相对标准偏差值?资讯攻略11-22 -
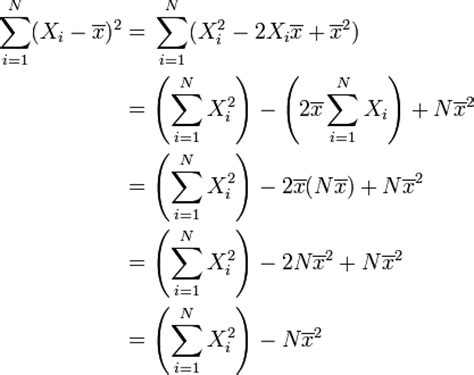 标准差公式是什么?资讯攻略10-29
标准差公式是什么?资讯攻略10-29 -
 揭秘:5.298四舍五入到小数点后两位的神奇结果资讯攻略11-14
揭秘:5.298四舍五入到小数点后两位的神奇结果资讯攻略11-14