揭秘长方体的独特特征
长方体是几何学中一种基本的三维形状,其广泛应用于建筑、工程、科学、数学及日常生活中。了解长方体的特征,不仅有助于我们更好地理解和运用这一形状,还能深化对空间几何的认识。长方体的特征可以从其定义、结构特点、表面积和体积计算、以及与其他几何形状的关联等多个维度来探讨。
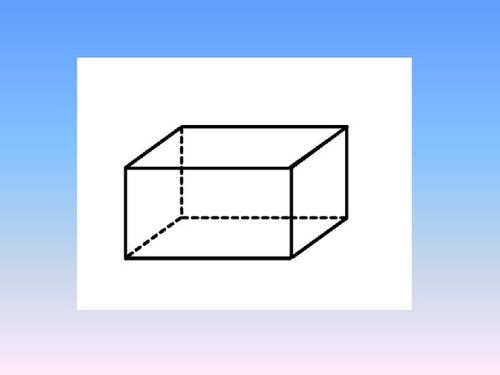
定义
长方体,又称矩形平行六面体或直平行六面体,是一种特殊的平行六面体,其六个面均为矩形。具体来说,长方体的三组对面(前后面、左右面、上下面)都是平行且相等的矩形。这一定义明确了长方体的两个基本特性:平行且相等的矩形面。
结构特点
长方体的结构特点主要体现在其边和角上。
1. 边:长方体有12条边。每组对面之间的4条边长度相等。例如,前后面之间的4条边(两条高和两条宽)长度相等,左右面之间的4条边(两条高和两条长)长度相等,上下面之间的4条边(两条长和两条宽)长度相等。这一特性使得长方体在视觉和物理上都呈现出一种对称美。
2. 角:长方体有8个顶点,每个顶点都是3条边的交点。由于长方体的三组对面都是平行的,因此每个角都是直角(90度)。这一特性确保了长方体的稳定性和规则的几何形状。
3. 面:如前所述,长方体有6个面,且每个面都是矩形。这些面可以是不同大小的矩形,但每组对面都是相等且平行的。
表面积和体积计算
长方体的表面积和体积是其重要的物理量,这两个量的计算有助于我们更好地理解长方体的空间特性。
1. 表面积:长方体的表面积是其所有面的面积之和。由于长方体有6个面,且每组对面都是相等的矩形,因此其表面积S可以通过以下公式计算:
\[S = 2lw + 2lh + 2wh\]
其中,l是长方体的长度,w是宽度,h是高度。这个公式反映了长方体表面积与其三个维度(长、宽、高)之间的直接关系。
2. 体积:长方体的体积是其内部空间的大小。由于长方体的每个面都是矩形,且所有角都是直角,因此其体积V可以通过以下公式计算:
\[V = lwh\]
这个公式表明,长方体的体积与其三个维度(长、宽、高)的乘积成正比。
与其他几何形状的关联
长方体作为三维几何形状的一种,与其他几何形状之间存在着密切的关联。
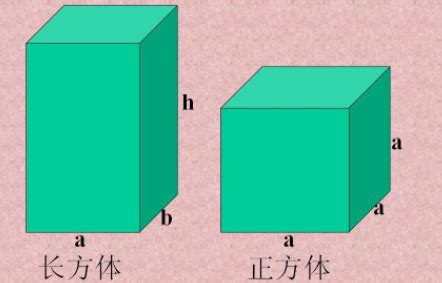
1. 与正方形的关系:当长方体的长、宽、高中有两个维度相等时,它就变成了一个特殊的长方体——正方体。此时,长方体的6个面都是正方形。正方体是长方体的一个特例,具有更高的对称性和规则性。
2. 与平行六面体的关系:平行六面体是长方体的一种更一般的形式,其六个面都是平行四边形。长方体作为平行六面体的一种特殊情况,具有更加严格的几何约束条件(即所有面都是矩形且所有角都是直角)。
3. 与圆柱体的关系:在某些情况下,长方体可以看作是由多个矩形围绕一个轴旋转而成的圆柱体的近似。当长方体的长度远大于其宽度和高度时,它就可以近似地看作是一个圆柱体。这种近似关系在工程学和材料科学中具有重要意义,因为它允许我们使用更简单的几何形状来估计和计算复杂形状的物理特性。
4. 与多面体的关系:长方体是一种特殊的多面体,具有规则、对称和易于计算的特点。多面体是一类广泛存在的三维几何形状,包括棱柱、棱锥等。长方体作为多面体的一种,在几何学和拓扑学中具有重要的地位和作用。
应用实例
长方体因其独特的结构和易于计算的特点,在建筑、工程、科学、数学及日常生活中得到了广泛应用。
1. 建筑:在建筑设计中,长方体是一种常见的形状选择。许多建筑物,如住宅、办公室、仓库等,都采用了长方体的形状。这种形状不仅易于建造和维护,而且能够提供稳定的结构支持和合理的空间布局。
2. 工程:在工程领域,长方体常用于制造各种机械零件和设备。例如,轴承、齿轮、箱体等部件通常采用长方体的形状,以确保其稳定性和可靠性。此外,长方体形状的容器和管道也广泛应用于液体和气体的储存和输送。
3. 科学:在科学研究中,长方体常被用作实验和观测的工具。例如,在物理学实验中,长方体形状的容器可以用于测量液体的密度、粘度等物理性质;在天文学观测中,长方体形状的望远镜镜筒可以提供稳定的支撑和清晰的视野。
4. 数学:在数学教育中,长方体是一个重要的教学工具。通过学习和掌握长方体的特征,学生可以更好地理解空间几何的概念和方法。此外,
- 上一篇: 定州市现在是否仍属于保定市?
- 下一篇: 揭秘:笙箫的正确发音怎么读?
-
 揭秘长方体周长计算的奥秘公式资讯攻略11-14
揭秘长方体周长计算的奥秘公式资讯攻略11-14 -
 揭秘长方体周长:轻松掌握计算公式资讯攻略11-13
揭秘长方体周长:轻松掌握计算公式资讯攻略11-13 -
 揭秘长方体表面积的神奇计算公式!资讯攻略12-07
揭秘长方体表面积的神奇计算公式!资讯攻略12-07 -
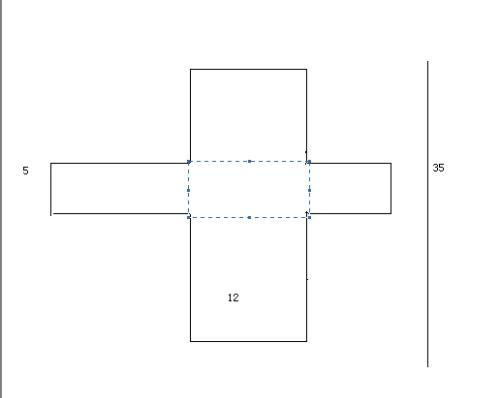 长方体展开图有几种常见的形式?资讯攻略11-12
长方体展开图有几种常见的形式?资讯攻略11-12 -
 揭秘雪獒的独特形态特征资讯攻略11-13
揭秘雪獒的独特形态特征资讯攻略11-13 -
 揭秘象鼻族人的独特生理特征:长度之谜解析资讯攻略01-25
揭秘象鼻族人的独特生理特征:长度之谜解析资讯攻略01-25












