揭秘三次函数的图像奥秘与独特性质

三次函数的图像和性质

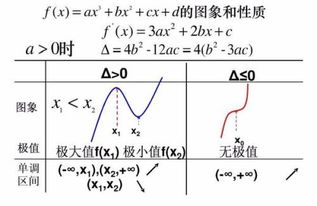
三次函数是高中数学的重要组成部分，研究三次函数的图像和性质有助于深入理解函数的性质以及其与几何图像之间的关系。下面我们就从多个方面探讨三次函数的图像和性质。

一、三次函数的概念与标准形式

三次函数指的是自变量最高次数为3的函数，一般形式为f(x) = ax³ + bx² + cx + d，其中a、b、c、d为常数，且a ≠ 0。三次函数的基本图像呈现为S形或反S形，这是由其导数的性质和奇偶性决定的。

二、三次函数的单调性

要判断三次函数的单调性，可以对其求一阶导数。对于函数f(x) = ax³ + bx² + cx + d，其一阶导数为f'(x) = 3ax² + 2bx + c。接下来，通过求解f'(x) = 0得到函数的拐点，即f'(x)的零点。若a > 0，则当x在某一拐点左侧时，f'(x) < 0，函数在此区间内单调递减；当x在该拐点右侧时，f'(x) > 0，函数在此区间内单调递增。反之，若a < 0，则单调性相反。因此，通过分析一阶导数可以清晰得出三次函数的单调区间。

三、三次函数的极值

根据单调性的分析，我们可以得出在拐点处，三次函数取得极值。由f'(x) = 0求得拐点x的值，再将x值代入原函数f(x)求得y值，即极值点的坐标。特别地，如果函数有多个拐点，需要分别求解每一个拐点处的极值。需要注意的是，并非所有拐点处的极值都是最大值或最小值，需要根据具体的函数形式进行判断。

四、三次函数的奇偶性

根据常数项d的不同取值，三次函数可以是奇函数、偶函数或非奇非偶函数。若d = 0，则函数满足f(-x) = -f(x)，此时函数为奇函数，图像关于原点对称；若函数满足f(-x) = f(x)，即函数的三次项系数a和常数项d同时为0（注意：这种特殊情况不常见，但存在），此时函数为偶函数，图像关于y轴对称；若d ≠ 0且函数既不满足奇函数也不满足偶函数的定义，则称该函数为非奇非偶函数。了解三次函数的奇偶性，可以帮助我们更快地描绘出其大致的图像特征。

五、三次函数的对称中心

对于一般形式的三次函数f(x) = ax³ + bx² + cx + d，我们可以通过代换和计算得到其对称中心的坐标。将f(x)的常数项d改写为-m²/4a + n，令x = t - b/3a，从而得到f(t)的简化形式，进一步通过对比和推导可以得到对称中心的坐标为(-b/3a, n - b²/12a)。需要注意的是，当b = 0时，对称中心位于y轴上，函数图像关于y轴对称。利用对称中心可以帮助我们更好地把握三次函数图像的整体走向和形状。

六、三次函数的图像

根据前面分析的单调性、极值、奇偶性和对称中心，我们可以尝试描绘出三次函数的图像。一般来说，三次函数的图像是连续不断的曲线，当a > 0时，图像呈现为先下降后上升（或先上升后下降）的S形；当a < 0时，图像呈现为先上升后下降（或先下降后上升）的反S形。具体图像特征还需要结合具体的a、b、c、d的值来确定。在实际绘图时，可以首先找到函数的拐点、极值点和对称中心，然后在这些点的基础上根据单调性连接曲线，得到最终的图像。

七、三次函数在实数域内的零点

判断三次函数在实数域内的零点个数是高中数学的一个重要问题。可以通过求解方程f(x) = 0（即ax³ + bx² + cx + d = 0）的根的个数来解决。这涉及到求解一元三次方程的判别式Δ，具体方法较为复杂，此处不赘述。需要注意的是，判别式Δ的正负直接决定了方程根的性质：当Δ > 0时，方程有三个不等的实根；当Δ = 0时，方程有三个实根，其中至少有两个根相等；当Δ < 0时，方程有一个实根和两个共轭虚根。因此，在求解三次函数零点时，首先需要计算判别式Δ，然后根据其正负性质进一步求解方程的根。

八、三次函数在函数问题中的应用

三次函数在数学问题和实际问题中有着广泛的应用。例如，在解决优化问题时，我们常会遇到三次函数，