如何绘制双曲线的准线
双曲线作为数学中的一个重要概念,其特性与几何形状让许多数学爱好者着迷。而在双曲线的众多特性中,准线的绘制是一个既有趣又富有挑战性的内容。本文将详细介绍如何绘制双曲线的准线,帮助那些对双曲线几何感兴趣的读者更好地理解和掌握这一技巧。
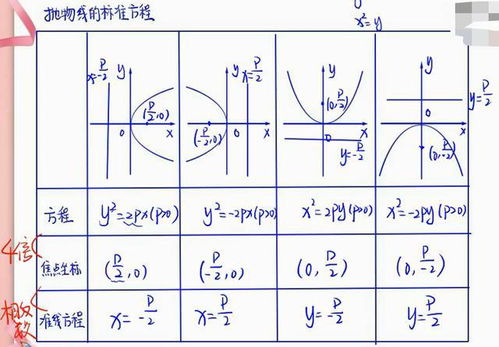
首先,我们需要明确什么是双曲线的准线。在平面内,到给定一点(称为焦点)及一直线(称为准线)的距离之比为常数e(e > 1)的点的轨迹称为双曲线。这个常数e被称为双曲线的离心率,而定直线就是双曲线的准线。根据双曲线的性质,我们知道双曲线有两条准线,分别位于双曲线的两侧,且与双曲线的焦点在同一直线上。

绘制双曲线的准线需要以下步骤:
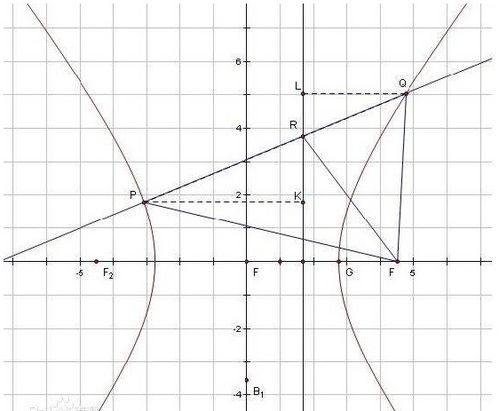
步骤一:确定双曲线的焦点和半焦距
首先,我们需要确定双曲线的两个焦点F1和F2。在双曲线的标准方程中,两个焦点通常位于x轴或y轴上,且它们之间的距离为2c,其中c是半焦距。如果焦点在x轴上,那么F1和F2的坐标分别为(-c, 0)和(c, 0);如果焦点在y轴上,那么F1和F2的坐标分别为(0, -c)和(0, c)。
步骤二:确定双曲线的实半轴长和虚半轴长
在双曲线的标准方程中,a表示实半轴长,b表示虚半轴长。实半轴长a决定了双曲线与x轴(或y轴)的交点距离原点的长度,而虚半轴长b则决定了双曲线的宽度。需要注意的是,a和b的值与双曲线的离心率e和半焦距c之间有关系:c² = a² + b²。
步骤三:计算准线的方程
双曲线的准线方程取决于焦点的位置。如果焦点在x轴上,那么左右准线的方程分别为x = ±a²/c;如果焦点在y轴上,那么上下准线的方程分别为y = ±a²/c。这里,a是实半轴长,c是半焦距。
步骤四:绘制准线
现在我们已经得到了双曲线的准线方程,接下来就可以在坐标系中绘制准线了。首先,在坐标系中画出x轴和y轴,并确定焦点的位置。然后,根据准线方程,在坐标系中画出与x轴(或y轴)平行的两条直线,这两条直线就是双曲线的准线。
为了更直观地理解双曲线的准线,我们可以通过一个具体的例子来进行说明。
示例:绘制焦点在x轴上的双曲线的准线
假设双曲线的焦点在x轴上,且F1(-5, 0),F2(5, 0),即半焦距c = 5。另外,我们假设实半轴长a = 4。根据c² = a² + b²,我们可以求出虚半轴长b = √(c² - a²) = √(25 - 16) = √9 = 3。
现在我们已经知道了焦点F1和F2的坐标,以及实半轴长a和虚半轴长b的值。接下来,我们可以计算准线的方程。由于焦点在x轴上,所以左右准线的方程分别为x = ±a²/c = ±4²/5 = ±16/5。
最后,我们在坐标系中画出x轴和y轴,并标出焦点F1和F2的位置。然后,根据准线方程x = ±16/5,我们在坐标系中画出与x轴平行的两条直线,这两条直线就是双曲线的准线。
绘制双曲线准线的几何方法
除了代数方法外,我们还可以通过几何方法来绘制双曲线的准线。这种方法更直观,适合那些对几何图形有深刻理解的读者。
方法一:利用焦点和垂直平分线
1. 作圆F1及圆上一点A。
2. 选择圆外一点F2。
3. 连接AF2,并作AF2的垂直平分线l。
4. 作直线AF1与l交于点P。
5. 当点A在圆上运动时,点P的轨迹将形成双曲线。同时追踪垂直平分线l,动直线l将包络出双曲线的准线。
需要注意的是,这种方法虽然直观,但在实际操作中可能比较复杂和繁琐。因此,对于初学者来说,还是推荐使用代数方法来计算并绘制双曲线的准线。
方法二:利用焦点和渐近线
双曲线的渐近线是与双曲线无限接近但永不相交的直线。对于焦点在x轴上的双曲线来说,其渐近线的方程为y = ±(b/a)x。
- 上一篇: 薄雾的正确读音
- 下一篇: 如何登录QQ邮箱网页版
-
 如何绘制最速曲线资讯攻略01-23
如何绘制最速曲线资讯攻略01-23 -
 如何在MATLAB中轻松绘制三维图形资讯攻略11-01
如何在MATLAB中轻松绘制三维图形资讯攻略11-01 -
 揭秘!抛物线焦点弦的神奇长度公式,让你秒变几何达人资讯攻略10-27
揭秘!抛物线焦点弦的神奇长度公式,让你秒变几何达人资讯攻略10-27 -
 Excel中创建曲线图的步骤指南资讯攻略10-30
Excel中创建曲线图的步骤指南资讯攻略10-30 -
 如何制作PPT中的曲线图?资讯攻略11-01
如何制作PPT中的曲线图?资讯攻略11-01 -
 如何绘制莱洛三角形?资讯攻略11-30
如何绘制莱洛三角形?资讯攻略11-30












