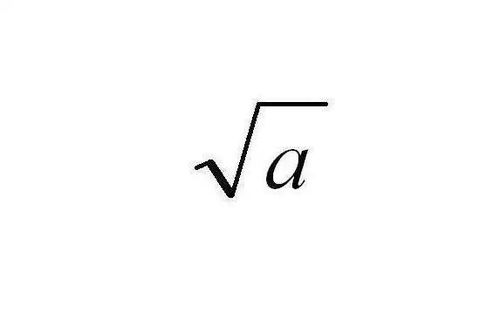3的平方根的数学表达式

在数学的世界里，探索数的性质与关系是一项既古老又充满挑战的任务。其中，平方根作为一个基本概念，连接了算术与几何，为理解更复杂的数学结构奠定了基础。当我们提到“3的平方根”时，实际上是在询问一个数，该数乘以自身等于3。这不仅仅是一个简单的数学运算，它还蕴含着丰富的数学思想、历史背景和实际应用。本文将从定义解析、数学表示、求解方法、历史发展、几何意义及实际应用等多个维度，深入探讨3的平方根如何书写及其背后的故事。

定义解析：平方根的概念

平方根，简而言之，是一个数的平方的逆运算。若一个数a的平方等于b（即a²=b），则称a是b的平方根。特别地，正数的平方根有两个值，一个正数和一个负数，因为这两个数相乘都能得到原来的正数。例如，4的平方根是±2，因为2²=4且(-2)²=4。对于非零实数，我们通常将正的平方根称为主平方根或算术平方根，而负的平方根则是对应的负值。因此，当我们谈论3的平方根时，实际上是指满足x²=3的x值，即x=±√3。

数学表示：符号与形式

在数学文献中，平方根通常使用根号（√）来表示。根号前的数字或表达式代表被开方的数，而根号本身则暗示着寻找一个数，该数的平方等于根号下的数。对于3的平方根，标准写法是√3，表示寻找一个数，其平方等于3。同时，为了完整表达正负两个解，我们会写作±√3。这种表示法简洁明了，是数学交流中的通用语言。

求解方法：近似计算与精确值

求解3的平方根，既可以通过直接计算得到近似值，也可以利用更高级的数学知识找到其精确表示。对于日常应用或初步学习，人们常常使用计算器或查表法得到近似值，如√3≈1.732。但在数学研究中，更关注于精确表达。在代数中，√3是一个无理数，即它不能表示为两个整数的比。尽管如此，我们仍可以通过级数展开、连分数或其他数学工具来逼近其精确值。此外，复数域内的平方根概念进一步扩展了平方根求解的范畴，允许我们找到形如a+bi（a,b为实数，i为虚数单位）的复数平方根。

历史发展：从古代到现代

平方根的概念可追溯至古代文明，如埃及、巴比伦和中国，它们在解决几何问题和计算面积时，无形中涉及到了平方根。古希腊数学家毕达哥拉斯学派在研究音乐和谐与几何比例时，也深刻理解了平方根的重要性。然而，对无理数的认识却经历了漫长而曲折的过程。毕达哥拉斯本人曾对无理数的存在表示震惊，认为它们违反了宇宙的和谐原则，这一发现甚至引发了学派内部的分裂。随着时间的推移，数学家们逐渐接受了无理数的概念，并开始系统研究包括3的平方根在内的无理数的性质。

几何意义：构造与直观理解

平方根不仅是一个代数概念，它在几何学中也有着直观的解释。以3的平方根为例，我们可以尝试通过几何作图来构造它。历史上，古希腊数学家使用了被称为“几何代数”的方法，通过构造特定的几何图形（如正方形、矩形等）来直观表示和求解平方根。虽然现代数学已经超越了这种直观的几何构造，但这种方法仍然为我们提供了一种理解平方根本质的直观方式。想象一个边长为√3的正方形，其面积即为3，这帮助我们直观地把握了3的平方根的含义。

实际应用：科学与工程的桥梁

3的平方根在自然科学、工程学以及经济学等多个领域都有着广泛的应用。在物理学中，它可能出现在描述振动、波动或量子态的方程中。在工程学中，当设计结构、计算应力或分析材料性能时，平方根运算也是不可或缺的。在经济学和金融学中，复利计算、股票价格预测及风险评估等模型也经常涉及平方根。此外，在计算机科学中，平方根是许多算法（如快速傅里叶变换、矩阵分解等）的核心组件。这些应用展示了3的平方根（及更广泛的平方根概念）作为连接理论与实践桥梁的重要作用。

结语

综上所述，3的平方根，以√3的形式简洁表达，是数学中一个既基本又深刻的概念。它不仅在代数、几何、数论等多个数学分支中占据核心地位，而且在自然科学、工程学、经济学等领域发挥着重要作用。从古代的几何构造到现代的精确计算，从无理数的发现到复数域内的扩展，3的平方根的历史演变见证了人类对自然界规律不断探索和深入理解的过程。在这个过程中，我们不仅学会了如何计算平方根，更重要的是，我们学会了如何运用数学的思维方式去分析问题、解决问题，以及如何在看似抽象的概念中找到与现实世界的联系。3的平方根，作为数学